Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, chọn Ox≡AB,O≡AOx≡AB,O≡A, chiều (+) A->B , mốc tgian là lúc 2 xe xuất phát
(xe B chuyển động chậm dần đều ngược chiều dương nên a'>0)
\(\Rightarrow\left\{{}\begin{matrix}xA=2t+\dfrac{1}{2}.0,2t^2\\xB=570-20t+\dfrac{1}{2}.0,4.t^2\end{matrix}\right.\) gặp nhau \(\Rightarrow xA=xB\Rightarrow t=30s\)
vị trí 2 xe gặp nhau cách A: \(S=xA=2.30+\dfrac{1}{2}.0,2.30^2=150m\)
b,\(\Rightarrow\left\{{}\begin{matrix}570=2t+\dfrac{1}{2}0,2t^2\\570=570-20t'+\dfrac{1}{2}0,4t'^2\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}t=66s\\t'=100s\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}v=vo+at=2+0,2.66=15,2m/s\\v'=vo'+a't'=60m/s\end{matrix}\right.\)

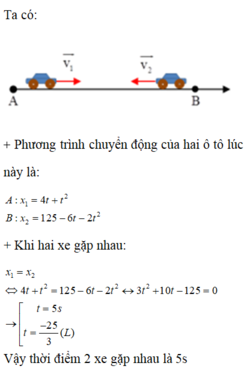
Chọn trục tọa độ nằm trên đường thẳng AB, chiều dương hướng từ A đến B, gốc tọa độ là A.
(xA = 0, xB = 125)
Vật thứ nhất,đi từ A đến B, có gia tốc +2 m/s², vận tốc đầu +4 m/s, tọa độ đầu 0,
có phương trình chuyển động là: x₁(t) = 1t² + 4t + 0, (t > 0
Vật thứ nhì , đi từ B đến A, có gia tốc −4 m/s², vận tốc đầu −6 m/s, tọa độ đầu +125,
có phương trình chuyển động là: x₂(t) = −2t² − 6t + 125, (t > 0)
(1a)
Thời điểm hai vật gặp nhau là thời điểm t > 0 sao cho
x₁(t) = x₂(t)
1t² + 4t = −2t² − 6t + 125, (t > 0)
3t² + 10t − 125 = 0, (t > 0)
Giải phương trình ta được t = 5 s
Vị trí lúc hai vật gặp nhau là
x₁(5) = 5² + 4×5 = 45 m
(1b)
Giả sử hai vật không va chạm khi gặp nhau và tiếp tục di chuyển với gia tốc không đổi đã cho.
Gọi v₀ là vận tốc đầu, v là vận tốc cuối sau khi đi hết quãng đường AB hay BA
Ta có công thức v² = v₀² + 2as
Đối với vật thứ nhất:
v₀ = +4 m/s, a = +2 m/s², s = (xB − xA) = 135 m,
Do đó:
v₁² = 4² + 2×2×125 = 516 (m/s)²,
Vì vật thứ nhất đi theo chiều dương nên v₁ > 0
v₁ = +√516 ≈ +22,72 m/s
Đối với vật thứ nhì:
v₀ = −6 m/s, a = −4 m/s², s = (xA − xB) = −135 m,
Do đó:
v₂² = 6² + 2×(-4)×(-125) = 1036 (m/s)²,
Vì vật thứ nhì đi theo chiều âm nên v₂ < 0
v₂ = −√1036 ≈ −32,19 m/s

Giải :
a. Theo bài ra gốc tọa độ tại A, chiều dương từ A đến B, gốc thời gian là lúc vật 1 qua A
Đối vật qua A : x 0 A = 0 m ; v 0 A = 20 m / s ; a A = − 1 m / s 2 ; x A = 20 t − 1 2 . t 2 ; v A = 20 − t
Đối vật qua B : x 0 B = 300 m ; v 0 B = − 8 m / s ; a B = 0 m / s 2 ; x B = 300 − 8 t
b. Khi hai vật gặp nhau nên ⇒ x A = x B ⇒ 20 t − 0 , 5 t 2 = 300 − 8 t ⇒ 0 , 5 t 2 − 28 t + 300 = 0
t 1 = 41 , 565 s ; t 2 = 14 , 435 s
Với t 1 = 41 , 565 s ⇒ x = 20.41 , 565 − 0 , 5.41 , 565 2 = − 3 , 2 , 5246 m L
Với t 2 = 14 , 435 s ⇒ x = 20.14 , 435 − 0 , 5.14 , 435 2 = 184 , 5154 m T / M
Vậy sau 14,435s thì hai vật gặp nhau v A = 20 − 14 , 435 = 5 , 565 m / s
khi hai vật gặp nhau vật A vẫn đang chuyển động
c. Khi vật 2 đến A ta có x B = 0 ⇒ 300 − 8 t = 0 ⇒ t = 37 , 5 s
Vật 1 dừng lại khi v A = 0 ⇒ 20 − t = 0 ⇒ t = 20 s ⇒ x A = 20.20 − 1 2 .20 2 = 200 m
Vậy khi vật 2 đến A thì vật một cách A là 200 m cách B là 100m

a) Phương trình chuyển động:
* Vật thứ nhất: x 1 = 5 t (m).
* Vật thứ hai: x 2 = 50 − t 2 (m).
b) Khi gặp nhau thì x 1 = x 2 ⇔ 5 t = 50 − t 2 hay t 2 + 5 t − 50 = 0 (*)
Giải phương trình (*) ta được: t 1 = 5 s; t 2 = − 10 s (loại).
Vị trí gặp nhau: x 1 = x 2 = 5.5 = 25 m.
Vậy hai vật gặp nhau tại thời điểm t = 5 s, tại vị trí cách A 25m.
c) Khi hai vật có vận tốc bằng nhau thì v 1 = v 2 = 5 m/s.
Phương trình vận tốc của vật thứ 2: v 2 = 2 t = 5 ⇒ t = 2 , 5 s .

Giải:
Chọn chiều dương là chiều từ đỉnh đến chân dốc, gốc toạ độ tại đỉnh A, gốc thời gian là lúc xe A xuống dốc.
Đối với xe A:
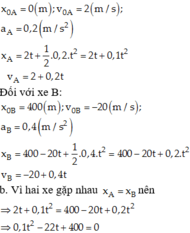

Thay thời gian loại nghiệm ta có hai thời điểm vật cách nhau 40m là