
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Các tam giác đều có công thức tính diện tích giống nhau: \(\dfrac{1}{2}.a.h\)
Dùng công thức tính diện tích tam giác thường vào tam giác vuông được nhé bạn

CT tính Sđáy của HCĐ:
Đáy là một tam giác cân: S = 1/2 . h cạnh đáy ( trong tam giác )
Đáy là một hình vuông : S = cạnh2 ( trong hình vuông )
#hoktot ❤️#
trong tam giác cân: 1/2.h. cạnh đáy(của tam giác) ( trong tam giác )

Cho tam giác ABC với đường cao AH. Ta dựng hình chữ nhật có một cạnh bằng một cạnh của tam giác ABC và có diện tích bằng diện tích tam giác ABC như hình dưới
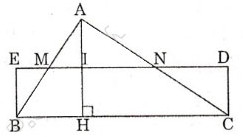
Ta có ∆EBM = ∆KAM và ∆DCN = ∆ KAN
Suy ra
SBCDE = SABC=  BC. AH
BC. AH
Ta đã tìm được công thức tính diện tích tam giác bằng một phương pháp khác.

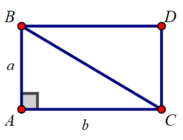
Muốn tính diện tích tam giác vuông ABC, ta dựng hình chữ nhật ABDC như trên
- ∆ABC = ∆DCB (hai cạnh góc vuông)
⇒SABC = SDCB (theo tính chất 1 diện tích đa giác) (1)
Đường chéo BC chia hình chữ nhật ABDC thành 2 phần là ∆ABC và ∆DCB
⇒SABDC = SABC + SDCB (theo tính chất 2 diện tích đa giác) (2)
Từ (1) và (2) ⇒ SABDC = 2SABC ⇒ SABC = 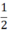 SABDC
SABDC
- ABDC là hình chữ nhật ⇒ SABDC = a.b
⇒ SABC = 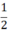 SABDC =
SABDC = 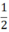 ab
ab

- Diện tích hình vuông cạnh a: S = a2
- Diện tích tam giác vuông có hai cạnh góc vuông a và b là: S = 0,5 ab
Tính chu vi. Chu vi là tổng chiều dài các mặt ngoài của bất kỳ hình học phẳng. Với một đa giác đều, chu vi có thể được tính bằng cách nhân chiều dài một cạnh với số cạnh (n).[1]
2
Xác định đường trung đoạn. Đường trung đoạn của một đa giác đều là đoạn thẳng vuông góc hạ từ tâm xuống một cạnh của nó. Đường trung đoạn hơi khó để tính hơn một chút so với chu vi.3
Biết công thức đúng. Diện tích của bất kỳ đa giác đều nào cũng được tính bằng công thức:Diện tích = (a x p)/2, trong đó, a là độ dài đường trung đoạn và p là chu vi đa giác đó.
4
Gán các giá trị a và p vào công thức và tính diện tích. Ví dụ, ta có một hình lục giác (6 cạnh) với mỗi cạnh (s) có độ dài bằng 10.Phần2
Hiểu khái niệm theo một cách khác
1
Hiểu rằng mỗi đa giác đều có thể được xem là một tập hợp các hình tam giác.Mỗi cạnh của đa giác đại diện cho cạnh đáy của tam giác, và số cạnh của đa giác là số hình tam giác có trong đa giác đó. Mỗi tam giác đều có chiều dài cạnh đáy, chiều cao và diện tích như nhau.[2]
2
Nhớ lại công thức tính diện tích hình tam giác. Diện tích của bất kỳ hình tam giác nào cũng bằng 1/2 tích số của cạnh đáy (ở đây chính là cạnh của đa giác) và chiều cao (chính là đường trung đoạn của đa giác đều).[3]
3
Phân tích sự tương đồng. Xin nhắc lại, công thức của đa giác đều là 1/2 tích số của đường trung đoạn và chu vi. Chu vi của đa giác là tích của chiều dài mỗi cạnh nhân với số cạnh (n); đối với một đa giác đều, n cũng đại diện cho số hình tam giác cấu thành đa giác đó. Vậy, công thức này không gì khác hơn chính là tổng diện tích của tất cả hình tam giác nằm trong đa giác đó.[4]