
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án cần chọn là: A
Ta có: 1 f = 1 d + 1 d ' → d = f d ' d ' − f ; d ' = f d d − f
Lại có: k = − d ' d → k = f f − d ; k = f − d ' f
=> A sai, B, C, D- đúng

∆ d = d 2 - d 1 ; ∆ d' = d 2 ' - d 1 ' = d 2 . f d 2 - f - d 1 . f d 1 - f
Suy ra
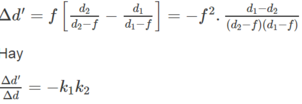

Đáp án B
Công thức xác định vị trí ảnh tạo bởi thấu kính: 1 f = 1 d + 1 d ' , với f là tiêu điểm của thấu kính; d, d’ lần lượt là khoảng cách từ vật và ảnh đến thấu kính

Công thức của thấu kính: 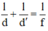
f là tiêu cự của thấu kính: f > 0 (TKHT); f < 0 (TKPK)
d là khoảng cách từ vật đến thấu kính d > 0 vật thật; d < 0 vật ảo.
d’ là khoảng cách từ ảnh đến ảnh thấu kính d’ > 0 ảnh thật; d’ < 0 ảnh ảo.

Công thức thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\)
Trong đó:
+ f là tiêu cự thấu kính, TK hội tụ f > 0, phân kỳ f <0
+ d là khoảng cách từ vật đến thấu kính, vật thật d > 0, vật ảo d < 0
+ d' là khoảng cách từ ảnh đến thấu kính, ảnh thật d' > 0, ảnh ảo d' < 0
Công thức lăng kính
\(sini_1=n.sinr_1;sini_2=n.sinr_2\\ A=r_1+r_2;D=I_1+I_2-A\)
Nếu các góc i và A nhỏ
\(i_1=nr_1;i_2=nr_2\\ A=r_1+r_2;D=\left(n-1\right)A\)
Độ tụ của thấu kính
\(D=\dfrac{1}{f}=\left(n-1\right)\left(\dfrac{1}{R_1}+\dfrac{1}{R_2}\right)\)
Vị trí ảnh
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'};d=\dfrac{d'f}{d'-f}\\ f=\dfrac{dd'}{d+d'};d'=\dfrac{df}{d-f}\)
Số phóng đại ảnh
\(\left|k\right|=\dfrac{A'B'}{AB};k=-\dfrac{d'}{d}=\dfrac{f}{f-d}=\dfrac{f-d'}{f}\)
Hệ 2 thấu kính đồng trục ghép sát
\(\dfrac{1}{f}=\dfrac{1}{f_1}+\dfrac{1}{f_2};D=D_1+D_2\)
Hệ 2 thấu kính đồng trục ghép cách nhau
- Quan hệ giữa 2 vai trò ảnh và vật của \(A_1'B_1'\)
\(AB\underrightarrow{L_1}A_1'B_1'\underrightarrow{L_2}A_2'B_2'\)
d_1 - d_1' ; d_2 - d_2'
Số phóng đại ảnh sau cùng
\(k=k_1k_2\)
Số bội giác
\(G=\dfrac{\alpha}{\alpha_o}\approx\dfrac{tan\alpha}{tan\alpha_o}\)
Kính lúp : ngắm chừng ở vô cực
\(G_{\infty}=\dfrac{OC_c}{f}=\dfrac{Đ}{f}\)
Kính hiển vi : ngắm chừng ở vô cực
\(G_{\infty}=\left|k_1\right|G_2=\dfrac{\delta D}{f_1f_2}\)
Kính thiên văn : ngắm chừng ở vô cực
\(G_{\infty}=\dfrac{f_1}{f_2}\)