![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

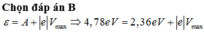
![]()

Động năng ban đầu cực đại của quang electron bứt ra từ mặt quả cầu:
\(\frac{mv^2_{max}}{2}=\frac{hc}{\lambda}-A=2,7.10^{-19}J\)
Gọi Q là điện tích của quả cầu, điện tích này phải là điện tích dương để giữ electron; điện tích Q phân bố đều trên mặt quả cầu, do đó điện thế trên mặt quả cầu là:
\(V=9.10^9.\frac{Q}{R}\). Trên quả cầu hình thành điện trường với các đường sức vuông góc với mặt cầu và hướng ra ngoài ( vì Q>0), điện trường này ngăn cản electron thoát ra khỏi quả cầu, công của điện trường cản là: \(W=eV=9.10^9.\frac{Qe}{R}\)
Muốn cho electron không thoát ra , công đó phải bằng động năng ban đầu cực đại của electron nghĩa là: \(9.10^9.\frac{Qe}{R}=\frac{mv^2_{max}}{2}\)
Thay số ta rút ra : \(Q=1,9.10^{-11}C\)

Khi tăng điện dung nên 2,5 lần thì dung kháng giảm 2,5 lần. Cường độ dòng trễ pha hơn hiệu điện thế \(\pi\text{/}4\) nên
\(Z_L-\frac{Z_C}{2,5}=R\)
Trường hợp đầu tiên thì thay đổi C để hiệu điện thế trên C cực đại thì
\(Z_LZ_C=R^2+Z^2_L\)
\(Z_LZ_C=\left(Z_L-\frac{Z_C}{2,5}\right)^2+Z^2_L\)
Giải phương trình bậc 2 ta được
\(Z_C=\frac{5}{4}Z_L\) hoặc \(Z_C=10Z_L\) (loại vì Zl-Zc/2.5=R<0)
\(R=\frac{Z_L}{2}\)
Vẽ giản đồ vecto ta được \(U\) vuông góc với \(U_{RL}\) còn \(U_C\) ứng với cạch huyền
Góc hợp bởi U và I bằng với góc hợp bởi \(U_L\) và \(U_{LR}\)
\(\tan\alpha=\frac{R}{Z_L}=0,5\)
\(\sin\alpha=1\text{/}\sqrt{5}\)
\(U=U_C\sin\alpha=100V\)
\(U_o=U\sqrt{2}=100\sqrt{2}V\)
chọn C

Chiếu bức xạ λ vào quả cầu kim loại cô lập về điện, thì điện thế cực đại là V, ta có: \(\dfrac{hc}{\lambda}=A_t+W_đ\), với \(W_đ=e.V\)
Chiếu bức xạ λ1: \(\dfrac{hc}{\lambda_1}=A_t+W_{đ1}=2W_{đ1}+W_{đ1}=3W_{đ1}=3.eV_1\)
\(\Rightarrow \dfrac{\lambda_1}{hc}=\dfrac{1}{3eV_1}\) (1)
Với \(A_t=2W_{đ1}=2.eV_1\)
Chiếu bức xạ λ2: \(\dfrac{hc}{\lambda_2}=A_t+W_{đ2}=2.eV_1+5eV_1=7eV_1\)
\(\Rightarrow \dfrac{\lambda_2}{hc}=\dfrac{1}{7eV_1}\) \(\Rightarrow \dfrac{\lambda_1-\lambda}{hc}=\dfrac{1}{7eV_1}\) (2)
Lấy (1) - (2) vế với vế: \(\Rightarrow \dfrac{\lambda}{hc}=\dfrac{4}{21.eV_1}\)
\(\Rightarrow \dfrac{hc}{\lambda}=5,25.eV_1=2eV_1+3,25eV_1=A_t+3,25eV_1\)
Suy ra điện thế cực đại của quả cầu là: \(3,25eV_1\)
Chọn C.

1) Năng lượng 3,5 eV chính là công thoát A. Ta có:
\(A=3,5eV=5,6.10^{-19}J\)
Bước sóng ánh sáng cần chiếu vào kim loại chính là giới hạn quang điện ứng với kim loại đó:
\(\lambda_0=\frac{hc}{\lambda}=0,355\mu m\)
2) Khi dùng ánh sáng đơn sắc trên chiếu vào catôt của tế bào quang điện, năng lượng của phôtôn chỉ dùng để tạo công thoát A nên vận tốc ban đầu \(v_0\) của quang electron bằng 0. Dưới tác dụng của điện trường, công của lực điện trường tác dụng lên electron từ catôt đến anôt cung cấp cho electron động năng khi đến anôt:
\(\frac{mv^2}{2}=eU\); suy ra vận tốc electron khi đến anôt:
\(v=\sqrt{\frac{2eU}{m}}=4.10^6m\text{/}s\)

Đáp án D
Điện thế cực đại của hai kim loại khi chiếu ánh sáng vào:
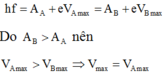
Khi chiếu bức xạ f’ vào quả cầu hợp kim:
![]()
![]()
![]()
Bước sóng của bức xạ điện từ chiếu vào quả cầu có độ lớn:
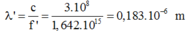

Đáp án D
Điện thế cực đại của hai kim loại khi chiếu ánh sáng vào:
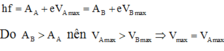
Khi chiếu bức xạ f’ vào quả cầu hợp kim:
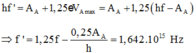
Bước sóng bức xạ điện từ chiếu vào quả cầu có độ lớn: