Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D

Ta có:
\(P=\dfrac{U_{1}^{2}}{Z_{1}^{2}}R\)
\(4P=\dfrac{U_{2}^{2}}{Z_{2}^{2}}R\)
\(\Rightarrow \dfrac{P}{4P}=\left( \dfrac{U_{1}}{U_{2}} \right)^{2}\left( \dfrac{Z_{2}}{Z_{1}} \right)^{2}\)
\(\Leftrightarrow \dfrac{1}{4}=\left(\dfrac{n_{1}}{n_{2}} \right)^{2}\left(\dfrac{Z_{2}}{Z_{1}} \right)^{2}\rightarrow Z_{2}=Z_{1}\)
Ta nghĩ đến bài toán f biến thiên có 2 giá trị của f mạch cho cùng 1 tổng trở.\(\Rightarrow n_{0}=\sqrt{n_{1}n_{2}}=\sqrt{2}n \)
Vậy khi roto quay với tốc độ \(\sqrt{2}n\) mạch xảy ra cộng hưởng.
Công suất: \(P_0=\dfrac{U_{0}^{2}}{R}\)
Lại có:
\(P=\dfrac{U_{1}^{2}}{Z_{1}^{2}}R=\dfrac{U_{1}^{2}}{2R^{2}}R=\dfrac{U_{1}^{2}}{2R}\) (Do \(Z_1=\sqrt 2.R\))
\(\Rightarrow \dfrac{P}{P_{0}}=\dfrac{U_{1}^{2}}{2U_{0}^{2}}=\dfrac{1}{2}\left(\dfrac{n_{1}}{n_{0}} \right)^{2}=\dfrac{1}{4} \Rightarrow P_{0}=4P\)
Vậy: \(P_0=4P\)
\(U_0=\omega\phi\)
\(P=I^2R=\left(\frac{U_0}{Z\sqrt{2}}\right)^2R=\frac{\omega^2\phi^2R}{2\left(R^2\left(\omega L-\frac{1}{\omega c}\right)^2\right)}\)
\(=\frac{\phi^2R}{2\left(\frac{R^2}{\omega^2}+\left(L-\frac{1}{\omega^2c}\right)^2\right)}=\frac{\phi^2R}{2\left(\frac{1}{\omega^4C^2}+\frac{R^2-2L}{\omega^2}+L^2\right)}\)
Do đó: \(\phi\) không đổi. Đặt : \(\frac{1}{\omega^2}=x\)
Xét f (x) \(=\frac{x^2}{C^2}+\left(R^2-2L\right)x+2L^2\)
=> P_max \(\Leftrightarrow x_0=\frac{2L-R^2}{2C^2}\)
Do P phụ thuộc hàm bậc 2 nên
\(P_1=P_2\Rightarrow x_1+x_2=2x_0\Leftrightarrow\frac{1}{\omega^2_1}+\frac{1}{\omega^2_2}=\frac{2}{\omega^2_0}\)
Mặt khác, tốc độ quay của rôto tỉ lệ thuận với tần số góc nên
\(\frac{1}{n^2_1}+\frac{1}{n^2_2}+\frac{1}{n^2_0}\Leftrightarrow n_0=2\frac{n^2_1n^2_2}{n^2_1+n^2_2}\)

+ Hiệu suất truyền tải điện năng được tính là: H=Ptt/P .
Đáp án B

Áp dụng: \(P=\dfrac{U^2}{R}\cos^2\varphi\)
\(\Rightarrow 160=\dfrac{U^2}{R}.0,4^2\) (1)
\(340=\dfrac{U^2}{R}.\cos^2\varphi\) (2)
Lấy (1) chia (2) vế với vế ta tìm đc \(\cos\varphi = 0,6\)
\(P_1=UI.cos\varphi=\frac{U^2.R}{Z.R}.cos\varphi=\frac{U^2}{R}.cos\varphi^2_1\)
\(P_2=UI.cos\varphi=\frac{U^2.R}{Z.R}.cos\varphi=\frac{U^2}{R}.cos\varphi^2_2\)
\(cos\varphi_2=0,6\)
đáp án B

Khi thang máy đi lên lực căng của dây cáp treo thang máy là:
T=(m1+m2)(g+a)(1)T=(m1+m2)(g+a)(1)
và lực ép của người lên mặt sàn thang máy có độ lớn:
N=m2(g+a)N=m2(g+a)
a) Trường hợp thang máy đi lên. Chọn chiều dương là chiều chuyển động. Dựa vào đồ thị ta nhận thấy:
- Ứng với đoạn OA trên đồ thị, thang máy chuyển động nhanh dần đều với gia tốc
a1=52=2,5m/s2a1=52=2,5m/s2
Theo (1)(1) lực căng của dây cáp bằng:
T1=(m1+m2)(g+a1)=6250NT1=(m1+m2)(g+a1)=6250N
Theo (2)(2) lực ép của người lên mặt sàn thang máy bằng:
N1=m2(g+a)=625NN1=m2(g+a)=625N
- Ứng với đoạn AB thăng máy chuyển động thẳng đều (a=0)(a=0) lực căng của dây cáp là: T2=(m1+m2)g=5000NT2=(m1+m2)g=5000N
và lực éo của người lên mặt sàn thang máy bằng:
N2=m2g=500NN2=m2g=500N
- Ứng với đoạn BC trên đồ thị, thang máy chuyển động chậm dần đều với gia tốc
a2=−52=−2,5m/s2a2=−52=−2,5m/s2
Lực căng của dây cáp là: T3=(m1+m2)(g+a2)=3750NT3=(m1+m2)(g+a2)=3750N
Lực ép của người lên mặt sàn là: N3=m2

Giải thích: Đáp án D
Phương pháp: Sử dụng lý thuyết về dao động điều hòa của CLLX
Cách giải:
+ Tần số góc: 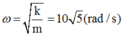
Độ giãn của lò xo ở VTCB: ![]()
+ Điểm treo của con lắc chịu được lực tối đa không quá 4N => Fđhmax ≤ 4N
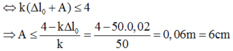

\(P=UI\cos\varphi\)
=> \(I=\frac{P}{U\cos\varphi}=\frac{P_i+I^2r}{U\cos\varphi}=\frac{80+I^2.32}{220.0.8}\)
=> phương trình bậc 2 của I và bấm máy tính
\(I_1=5\)(loại vì hiệu suất \(H=\frac{80}{UI\cos\varphi}=9,09\%\))
hoặc \(I_2=0.5\) (chọn)
=> \(I_0=I\sqrt{2}=0,5\sqrt{2}A.\)
chọn đáp án D.
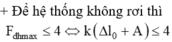
Mk yêu cầu nêu rõ thông số xe mà