Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

C không đúng vì để làm được như vậy thì cần qua một cơ cấu hệ phức tạp chứ không phải là đơn giản.
Đơn giản nhất theo mình nghĩ là tác dụng lên hệ một dao động tuần hoàn theo thời gian (là dao động cưỡng bức)
@Nguyễn Quang Hưng: bạn ơi nếu đáp án D mình tưởng xe giảm xóc càng lâu càng tốt chứ. để giúp êm xe mà.
như vậy có lợi sao cần phải tắt dần nhanh

Chọn đáp án D
@ Lời giải:
+ Giả sử biên độ dao động ban đầu là A, sau chu kì thứ nhất biên độ dao động giảm 2% nên biên độ còn lại là A 1 = 0 , 98 A , sau chu kì thứ hai biên độ giảm tiếp 2% nên A 2 = 0 , 98 A 1 = 0 , 98 2 A
+ Phần trăm cơ năng mất đi trong hai chu kì là:
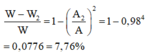

Hai điểm có cùng biên độ 2 mm đối xứng nhau qua nút gần nhất và hai điểm có biên độ 3 mm nằm đồi xứng nhau qua bụng gần nhất. Áp dụng công thức tình biên độ điểm, ta có hệ phương trình:
Gọi biên độ sóng tại bụng là 2a.
Ta có : \(\frac{1}{a^2}=\frac{9}{4a^2}=1\rightarrow a=\frac{2}{\sqrt{13}}\)
Xét: \(2a\sin\frac{2\pi x}{\lambda}=2\rightarrow2\lambda=54cm\Rightarrow\lambda=27cm\)
Vậy chọn đáp án A.
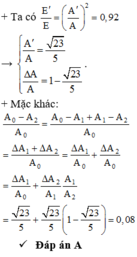
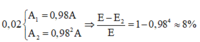
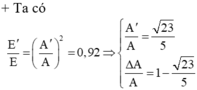
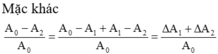
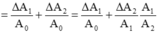
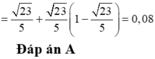

Đáp án B
Phương pháp: Sử dụng công thức tính cơ năng.
Cách giải:
Tỷ lệ cơ năng sau và trước sau 1 chu kì:
=> A' = 97,5%A
=> Phần trăm biên độ giảm sau mỗi chu kì bằng 100 – 97,5 = 2,5%