K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
giups mk bài toán nha
25 tháng 5 2022
Bài 3.2:
a: ta có: |x+9|=2x
\(\Leftrightarrow\left\{{}\begin{matrix}x>=0\\\left(2x\right)^2-\left(x+9\right)^2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\left(2x-x-9\right)\left(2x+x+9\right)=0\end{matrix}\right.\)
=>x=9
b: ta có: \(\left|5x\right|=3x-2\)
\(\Leftrightarrow\left\{{}\begin{matrix}x>=\dfrac{2}{3}\\\left(5x-3x+2\right)\left(5x+3x-2\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=\dfrac{2}{3}\\\left(2x+2\right)\left(8x-2\right)=0\end{matrix}\right.\)
hay \(x\in\varnothing\)
c: Ta có: \(\Leftrightarrow\left|x+6\right|=2x+9\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-\dfrac{9}{2}\\\left(2x+9-x-6\right)\left(2x+9+x+6\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x>=-\dfrac{9}{2}\\\left(x+3\right)\left(3x+15\right)=0\end{matrix}\right.\Leftrightarrow x=-3\)
d: \(\Leftrightarrow\left|2x-3\right|=21-x\)
\(\Leftrightarrow\left\{{}\begin{matrix}x< =21\\\left(21-x-2x+3\right)\left(21-x+2x-3\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x< =21\\\left(24-3x\right)\left(x+18\right)=0\end{matrix}\right.\Leftrightarrow x\in\left\{8;-18\right\}\)
NT
1
20 tháng 7 2017
Vẽ Oz // Ax
=> \(\widehat{xAO}=\widehat{AOz}\left(soletrong\right)=50^0\)
Ta có: \(\widehat{AOz}+\widehat{zOB}=\widehat{AOB}\)
hay \(50^0+\widehat{zOB}=80^0\)
\(\widehat{zOB}=80^0-50^0\)
=> \(\widehat{zOB}=30^0\)
Vì Ax // Oz
mà Ax // By
=> Oz // By
=> \(\widehat{OBy}=\widehat{zOB}\left(soletrong\right)=30^0\)
=> \(\widehat{OBy}=30^0\)
HH
26 tháng 5 2018
a/ \(\Delta ADE\)vuông và \(\Delta ADF\)vuông có:
\(\widehat{EAD}=\widehat{DAF}\)(AD là đường phân giác của \(\Delta ABC\))
Cạnh huyền AD chung
=> \(\Delta ADE\)vuông = \(\Delta ADF\)vuông (cạnh huyền - góc nhọn)
=> DE = DF (hai cạnh tương ứng) (đpcm)
b/ \(\Delta ABD\)và \(\Delta ACD\)có:
AB = AC (\(\Delta ABC\)cân tại A)
\(\widehat{EAD}=\widehat{DAF}\)(AD là đường phân giác của \(\Delta ABC\))
Cạnh AD chung
=> \(\Delta ABD\)= \(\Delta ACD\)(c. g. c)
Ta có AB = AC (\(\Delta ABC\)cân tại A)
=> A thuộc đường trung trực của BC
=> AD \(\perp\)BC (đpcm)
c/ Ta có AD là đường phân giác của \(\Delta ABC\)
=> \(\widehat{DAB}=\frac{\widehat{BAC}}{2}=\frac{80^o}{2}=40^o\)(tính chất tia phân giác)
và \(\widehat{EDA}=90^o-\widehat{DAB}\)(\(\Delta ADB\)vuông tại D)
=> \(\widehat{EDA}=90^o-40^o=50^o\)
Ta lại có: \(\widehat{DAB}< \widehat{EDA}\)(vì 40o < 50o)
=> DE < AE (quan hệ giữa góc và cạnh đối diện trong tam giác)
và \(\hept{\begin{cases}DA< AE\\DA< DE\end{cases}}\)(quan hệ giữa đường vuông góc và đường xiên)
=> DA < DE < AE (đpcm)
26 tháng 5 2018
a)Xét tam giác EAD và FAD có
AÊD= góc AFD=90*
AD là cạnh chung
góc EAD=góc FAD(tam giác ABC cân)
=>tam giác ...=...(cạnh huyền-góc nhọn)
=>DE=DF
b)Xét tam giác ABD và ACD có
BA=CA(gt)
BÂD=CÂD(gt)
AD là cạnh chung
=>tam giác ...=...(c-g-c)
=>góc BDA=CDA
mà BDA+CDA=180*
=>BDA=CDA=180*/2=90*
=>AD vuông góc với BC
c) Xét tam giác AED có: AÊD+EÂD+ góc EDA=180*
=>90*+(80*/2)+góc EAD=180*
=>90*+40*+góc EAD=180*
=>góc EAD=180*-(90*+40*)
=>góc EAD=50*
ta có:EÂD<góc ADE<AÊD(40*<50*<90*)
=>ED<AE<AD
Vậy, ED<AE<AD.
S
3 tháng 12 2019
Có: y tỉ lệ nghịch với x theo hệ số tỉ lệ a => \(y=\frac{a}{x}\) \(\left(a\ne0\right)\)
x tỉ lệ thuận vs z theo hệ số tỉ lệ k => \(x=k.z\) \(\left(k\ne0\right)\)
\(\Rightarrow y=\frac{a}{k.z}\Rightarrow y.z=\frac{a}{k}\)
Vậy y tỉ lệ nghịch với z theo hệ số \(\frac{a}{k}\)
NT
7
VT
22 tháng 8 2016
Không thuộc tập hợp nào cả. Vì N là tập hợp số tự nhiên, Z là tập hợp gồm số nguyên dươn, số nguyên âm và số 0, còn Q là tập hợp các số hữu tỉ viết được dưới dạng phân số a/b mà a, b thuộc Z.
5 tháng 12 2017
Bài 39. Vẽ trên cùng một hệ trục toạ độ OxyOxy đồ thị của các hàm số:
a) y=xy=x; b) y=3xy=3x;
c) y=−2xy=−2x; d) y=−xy=−x.
Hướng dẫn giải:
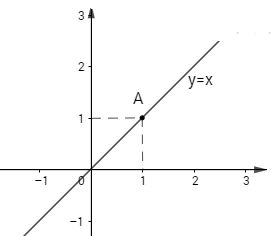
a) y=x
- Vẽ hệ trục tọa độ Oxy
- Cho x=1 được ⇒A(1;1) thuộc đồ thị hàm số y =x
Vậy đường thẳng OA là đồ thị của hàm số đã cho.
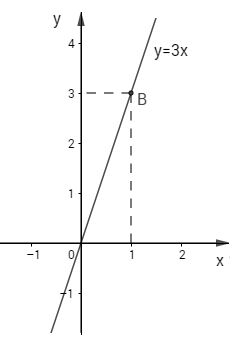
b) y=3x
- Vẽ hệ trục tọa độ Oxy
- Cho x=1 được y=3 ⇒B(1;3) thuộc đồ thị hàm số y=3x
Vậy đường thẳng OBlà đồ thị của hàm số đã cho.
ticks hộ mình nhé
Mình nghĩ là không có tập hợp này đâu.
Mình nghĩ có tập hợp N* thì chắc cũng có tập hợp Z*