
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2:
n) Ta có: \(N=\dfrac{4}{2\cdot4}+\dfrac{4}{4\cdot6}+\dfrac{4}{6\cdot8}+...+\dfrac{4}{2014\cdot2016}\)
\(=2\left(\dfrac{2}{2\cdot4}+\dfrac{2}{4\cdot6}+\dfrac{2}{6\cdot8}+...+\dfrac{2}{2014\cdot2016}\right)\)
\(=2\left(\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{8}+...+\dfrac{1}{2014}-\dfrac{1}{2016}\right)\)
\(=2\cdot\left(\dfrac{1}{2}-\dfrac{1}{2016}\right)\)
\(=2\cdot\dfrac{1007}{2016}=\dfrac{1007}{1008}\)
o) Ta có: \(\dfrac{1}{18}+\dfrac{1}{54}+\dfrac{1}{108}+...+\dfrac{1}{990}\)
\(=\dfrac{1}{3\cdot6}+\dfrac{1}{6\cdot9}+\dfrac{1}{9\cdot12}+...+\dfrac{1}{30\cdot33}\)
\(=\dfrac{1}{3}\left(\dfrac{3}{3\cdot6}+\dfrac{3}{6\cdot9}+\dfrac{3}{9\cdot12}+...+\dfrac{3}{30\cdot33}\right)\)
\(=\dfrac{1}{3}\left(\dfrac{1}{3}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{12}+...+\dfrac{1}{30}-\dfrac{1}{33}\right)\)
\(=\dfrac{1}{3}\left(\dfrac{1}{3}-\dfrac{1}{33}\right)\)
\(=\dfrac{1}{3}\cdot\dfrac{10}{33}=\dfrac{10}{99}\)
a) Ta có: \(\left(6\dfrac{4}{9}+3\dfrac{7}{11}\right)-4\dfrac{4}{9}\)
\(=\dfrac{58}{9}+\dfrac{40}{11}-\dfrac{40}{9}\)
\(=2+\dfrac{40}{11}=\dfrac{62}{11}\)
Bài 2:
b) Ta có: \(10\dfrac{1}{5}-5\dfrac{1}{2}\cdot\dfrac{60}{11}+3:15\%\)
\(=\dfrac{51}{5}-\dfrac{11}{2}\cdot\dfrac{60}{11}+3:\dfrac{3}{20}\)
\(=\dfrac{51}{5}-30+20\)
\(=\dfrac{51}{5}-10=\dfrac{1}{5}\)
c) Ta có: \(\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+\dfrac{2}{7\cdot9}+...+\dfrac{2}{97\cdot99}\)
\(=\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+...+\dfrac{1}{97}-\dfrac{1}{99}\)
\(=\dfrac{1}{3}-\dfrac{1}{99}\)
\(=\dfrac{32}{99}\)

Trả lời:
\(\frac{4}{7.9}+\frac{4}{9.11}+...+\frac{4}{107.109}\)
\(=\frac{2.2}{7.9}+\frac{2.2}{9.11}+...+\frac{2.2}{107.109}\)
\(=2.\left(\frac{2}{7.9}+\frac{2}{9.11}+...+\frac{2}{107.109}\right)\)
\(=2.\left(\frac{1}{7}-\frac{1}{9}+\frac{1}{9}-\frac{1}{11}+...+\frac{1}{107}-\frac{1}{109}\right)\)
\(=2.\left(\frac{1}{7}-\frac{1}{109}\right)=2.\frac{102}{763}=\frac{204}{763}\)

a: =>x-4=0 hoặc x+5=0
=>x=4 hoặc x=-5
b: =>39/7:x=13
hay x=3/7
c: \(\Leftrightarrow\left(4.5-2x\right)=\dfrac{11}{4}:\dfrac{4}{9}=\dfrac{99}{16}\)
\(\Leftrightarrow2x=-\dfrac{27}{16}\)
hay x=-27/32
d: \(\Leftrightarrow x\cdot\dfrac{19}{15}=684\)
hay x=540
a. \(\left[{}\begin{matrix}x-4=0\\x+5=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-5\end{matrix}\right.\)
b.\(\Leftrightarrow\dfrac{39}{7}:x=13\)
\(\Leftrightarrow x=13.\dfrac{39}{7}\)
\(\Leftrightarrow x=\dfrac{507}{7}\)
c.\(\Leftrightarrow4,5-2x=\dfrac{99}{16}\)
\(\Leftrightarrow-2x=\dfrac{27}{16}\)
\(\Leftrightarrow x=-\dfrac{27}{32}\)

\(\Rightarrow A=\frac{6n+2-5}{3n+1}=\frac{2\left(3n+1\right)}{3n+1}-\frac{5}{3n+1}\)=\(2-\frac{5}{3n+1}\)
Để A có giá trị nguyên \(\Leftrightarrow5⋮3n+1\Rightarrow3n+1\in\left\{-5;-1;1;5\right\}\)
\(\Rightarrow3n\in\left\{-6;-2;0;4\right\}\Rightarrow n\in\left\{-2;-\frac{2}{3};0;\frac{4}{3}\right\}\) Mà n \(\in Z\)
\(\Rightarrow n\in\left\{-2;0\right\}\)
Trả lời:
Ta có: \(\frac{6n-3}{3n+1}=\frac{2\left(3n+1\right)-5}{3n+1}=\frac{2\left(3n+1\right)}{3n+1}-\frac{5}{3n+1}=2-\frac{5}{3n+1}\)
Để A là số nguyên thì \(\frac{5}{3n+1}\)là số nguyên
=> \(5⋮3n+1\) hay \(3n+1\inƯ\left(5\right)\)\(=\left\{\pm1;\pm5\right\}\)
Ta có bảng sau:
| 3n+1 | 1 | -1 | 5 | -5 |
| 3n | 0 | -2 | 4 | -6 |
| n | 0 | \(\frac{-2}{3}\)(loại) | \(\frac{4}{3}\)(loại) | -2 |
Vậy n \(\in\){ 0 ; -2 } thì A có giá trị nguyên

S=-a+b+c-c+b-a-a-b
S=(-a+a)+(-b+b)+(-c+c)+(b-a)
S=b-a
Vì a > b nên b-a <0 do đó |S|=|b-a|=-(b-a) hay |S|=a-b
NHỚ K MÌNH NHA ! CHÚC BẠN HỌC TỐT !

Câu 7:
Gọi số học sinh là x
Theo đề, ta có: \(x\in BC\left(3;4;6;8\right)\)
hay x=72

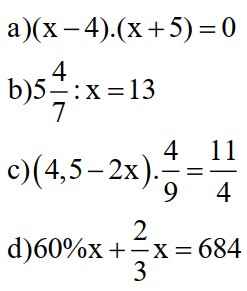 mọi người giúp e với hnay e gặp quá nhiều bài khó nên rất nguy mong mọi người giúp đỡ ạ
mọi người giúp e với hnay e gặp quá nhiều bài khó nên rất nguy mong mọi người giúp đỡ ạ
bài đâu bn
có thấy gì đâu bạn