GA
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
13 tháng 4 2023
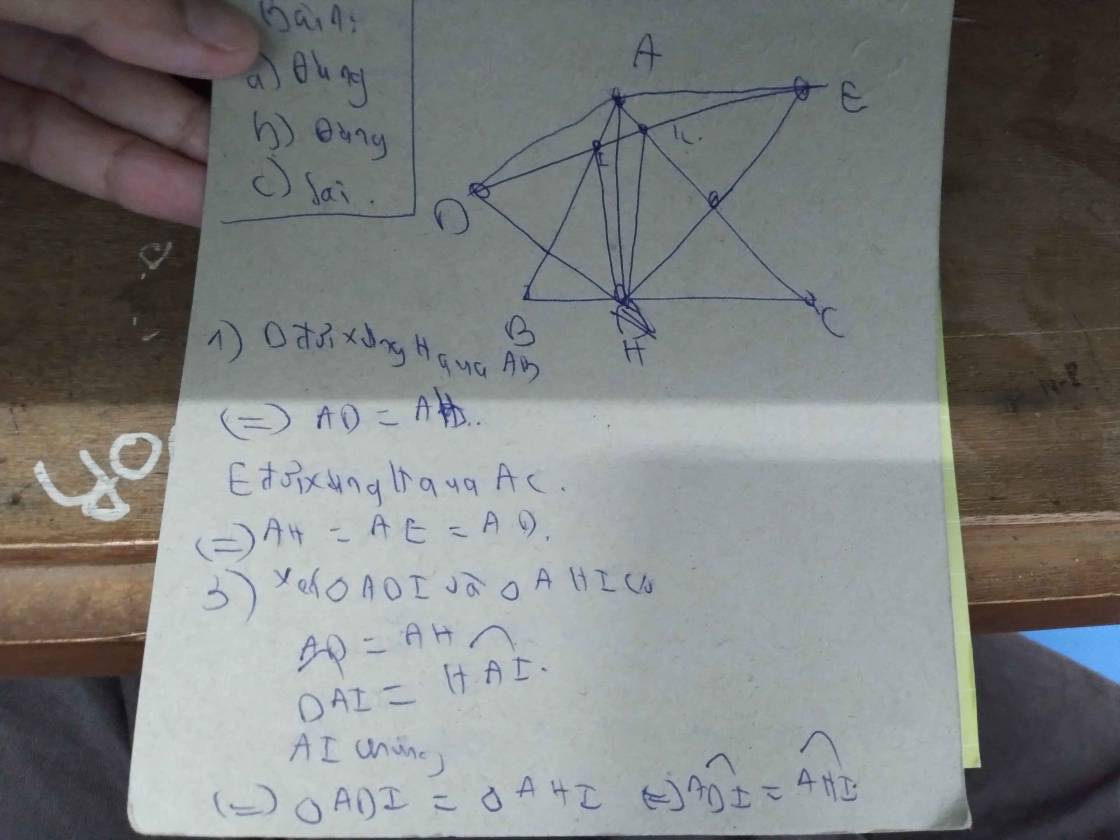
1: H đối xứng D qua AB
=>AH=AD
H đối xứng E qua AC
=>AH=AE
=>AH=AD=AE
3: Xét ΔAIH và ΔADI có
AH=AD
góc HAI=góc DAI
AIchung
=>ΔAIH=ΔAID
=>góc AHI=góc ADI=góc ADE
Xét ΔAHK và ΔAEK có
AH=AE
góc HAK=góc EAK
AK chung
=>ΔAHK=ΔAEK
=>góc AEK=góc AHK=góc AED
=>góc AHK=góc AHI
=>HA là phân giác của góc IHK
25 tháng 12 2016
Lâu rồi k giải toán, giờ trở lại vs Toán thân iu
Ta có hình vẽ:
a/ Xét tam giác ABD và tam giác CMD có:
AD = DC (vì D là trung điểm AC)
góc ADB = góc CDM (đối đỉnh)
DB = DM (GT)
Vậy tam giác ABD = tam giác CMD (c.g.c)
=> AB = CM (2 cạnh tương ứng)
Ta có: tam giác ABD = tam giác CMD
=> góc BAC = góc MCA (2 góc tương ứng)
b/ Xét tam giác AMD và BCD có:
AD = DC (vì D là trung điểm AC)
góc ADM = góc BDC (đối đỉnh)
DM = DB (GT)
Vậy tam giác AMD = tam giác BCD (c.g.c)
=> góc MAD = góc DCB (2 góc tương ứng)
Mà 2 góc này đang ở vị trí so le trong
=> AM // BC (đpcm)
c/ Xét tam giác ABC và tam giác AMC có:
AC: cạnh chung
AB = CM (do tam giác ABD = tam giác CMD)
AM = BC (do tam giác AMD = tam giác BCD)
=> tam giác ABC = tam giác AMC (c.c.c)
d/ Ta có: AB = CM (câu a)
Mà I là trung điểm AB
và K là trung điểm CM
=> AI = IB = MK = KC
Xét tam giác IAD và tam giác KCD có:
AI = CK (đã chứng minh trên)
góc BAC = góc MCA (câu a)
AD = DC (vì D là trung điểm AC)
=> tam giác IAD = tam giác KCD (c.g.c)
=> góc IDA = góc KDC (2 góc tương ứng)
Ta có: \(\widehat{ADM}\)+\(\widehat{MDK}\)+\(\widehat{KDC}\)=1800
=> góc ADM + góc MDK + góc IDA = 1800
=> góc IDK = 1800
hay K,D,I thẳng hàng
Khi đường thẳng d là đường trung trực của đoạn thẳng AB thì điểm A đối xứng với điểm B qua đường thẳng d. Khi đó đường thẳng d gọi là trục đối xứng của hai điểm A và B. Nói cách khác, hai điểm được gọi là đối xứng với nhau qua một đường thẳng nếu đường thẳng đó là đường trung trực của đoạn thẳng nối hai điểm đó.