

![]()
![]()
![]()
![]()
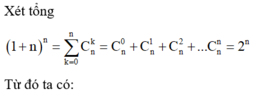
![]()
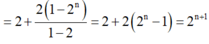
![]()
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


![]()
![]()
![]()
![]()
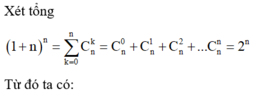
![]()
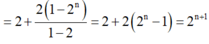
![]()
![]()
![]()
![]()
![]()

Bạn ghi đề bài riêng biệt, rõ ràng ra được ko
Chứ thế này thì ko biết đâu mà lần cả

2.
Phương trình (C) là đường tròn khi và chỉ khi \(m^2-2m>0\Rightarrow\left[{}\begin{matrix}m>2\\m< 0\end{matrix}\right.\)
Khi đó (C) là đường tròn tâm \(A\left(0;1\right)\) bán kính \(R=\sqrt{m^2-2m}\)
Pt (C'): \(\left(x-1\right)^2+y^2=2m^2-3m\)
(C') là pt đường tròn khi và chỉ khi \(2m^2-3m>0\Rightarrow\left[{}\begin{matrix}m>\frac{3}{2}\\m< 0\end{matrix}\right.\)
Khi đó (C') là đường tròn tâm \(B\left(1;0\right)\) bán kính \(\sqrt{2m^2-3m}\)
Tồn tại một phép tịnh tiến biến (C) thành (C') khi và chỉ khi (C) và (C') có cùng bán kính
\(\Leftrightarrow\sqrt{m^2-2m}=\sqrt{2m^2-3m}\)
\(\Leftrightarrow m^2-2m=2m^2-3m\)
\(\Leftrightarrow m^2-m=0\Rightarrow\left[{}\begin{matrix}m=0\left(l\right)\\m=1\left(l\right)\end{matrix}\right.\)
Vậy không tồn tại m thỏa mãn
1.
Phép tịnh tiến theo \(\overrightarrow{v}=\left(a;b\right)\) biến d thành d' cùng phương với d
\(\Rightarrow\) Phương trình d' có dạng: \(x+y+c=0\)
Đường tròn (C) tâm \(I\left(3;3\right)\) bán kính \(R=\sqrt{2}\)
Do d' tiếp xúc (C) \(\Leftrightarrow d\left(I;d'\right)=R\)
\(\Leftrightarrow\frac{\left|3+3+c\right|}{\sqrt{1^2+1^2}}=\sqrt{2}\Leftrightarrow\left|c+6\right|=2\)
\(\Rightarrow\left[{}\begin{matrix}c=-8\\c=-4\end{matrix}\right.\)
Có 2 đường thẳng d' thỏa mãn: \(\left[{}\begin{matrix}x+y-8=0\\x+y-4=0\end{matrix}\right.\)
Ứng với đó ta có 2 dạng vecto \(\overrightarrow{v}=\left(a;8-a\right)\) hoặc \(\overrightarrow{v}=\left(a;4-a\right)\)

Câu 1.
\(y = \dfrac{{n + \sin 2n}}{{n + 5}} = \dfrac{{\dfrac{n}{n} + \dfrac{{\sin 2n}}{n}}}{{\dfrac{n}{n} + \dfrac{5}{n}}} = \dfrac{{1 + \dfrac{{2.\sin 2n}}{{2n}}}}{{1 + \dfrac{5}{n}}}\\ \Rightarrow \lim y = \dfrac{{1 + 0}}{{1 + 0}} = 1 \)
Câu 2.
\(\lim \dfrac{{3\sin n + 4\cos n}}{{n + 1}}\)
Vì \( - 1 \le \sin n \le 1; - 1 \le \cos n \le 1 \Rightarrow \) khi \(x \to \infty \) thì \(3\sin n + 4{\mathop{\rm cosn}\nolimits} = const \)
\(\Rightarrow T = \lim \dfrac{{3\sin n + 4\cos n}}{{n + 1}} = 0 \)
Chú thích: $const$ là kí hiệu hằng số, giống như dạng giới hạn L/vô cùng.

Xét khai triển:
\(\left(1+x\right)^n=C_n^0+xC_n^1+x^2C_n^2+...+x^nC_n^n\)
Đạo hàm 2 vế:
\(n\left(1+x\right)^{n-1}=C_n^1+2xC_n^2+...+n.x^{n-1}C_n^n\)
Thay \(x=1\)
\(\Rightarrow n.2^{n-1}=C_n^1+2C_n^2+...+nC_n^n\)
\(\Rightarrow n.2^{n-1}+1=C_n^0+C_n^1+2C_n^2+...+nC_n^n\)
\(\Rightarrow S=n.2^{n-1}+1\)

a/ Đề không rõ ràng bạn
Từ câu b trở đi, dễ dàng nhận ra tất cả các hàm số đều liên tục trên R
b/ Xét \(f\left(x\right)=x^3+3x^2-1\)
Ta có: \(f\left(-3\right)=-1\) ; \(f\left(-2\right)=3\)
\(\Rightarrow f\left(-3\right).f\left(-2\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm trên \(\left(-3;-2\right)\)
\(f\left(0\right)=-1\Rightarrow f\left(-2\right).f\left(1\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm trên \(\left(-2;0\right)\)
\(f\left(1\right)=3\Rightarrow f\left(0\right).f\left(1\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm trên \(\left(0;1\right)\)
\(\Rightarrow f\left(x\right)\) luôn có 3 nghiệm phân biệt
c/\(f\left(x\right)=m\left(x-1\right)^3\left(m^2-4\right)+x^4-3\)
\(f\left(-2\right)=13\) ; \(f\left(1\right)=-2\)
\(\Rightarrow f\left(-2\right).f\left(1\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm trên \(\left(-2;1\right)\)
\(f\left(2\right)=13\Rightarrow f\left(1\right).f\left(2\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm trên \(\left(1;2\right)\)
\(\Rightarrow f\left(x\right)\) luôn có ít nhất 2 nghiệm
d/ \(f\left(x\right)=5sin3x+x-10\)
\(f\left(0\right)=-10\)
\(f\left(4\pi\right)=4\pi-10\)
\(\Rightarrow f\left(0\right).f\left(4\pi\right)=-10\left(4\pi-10\right)< 0\)
\(\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(0;4\pi\right)\) hay \(f\left(x\right)\) luôn có nghiệm