Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Có vô số phép tịnh tiến biến một đường thẳng thành một đường thẳng song song với nó.
Khi đó, vecto tịnh tiến có giá song song đường thẳng d.

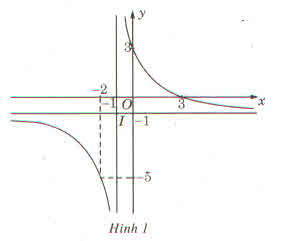
a) (H) có các đường tiệm cận là:
- Tiệm cận ngang y = -1
- Tiệm cận đứng x = -1
hai đường tiềm cận này cắt nhau tại điểm I(-1; -1).
Hình (H') có hai đường tiệm cận cắt nhau tại I'(2;2) nên ta cần phép tịnh tiến theo vector \(\overrightarrow{II'}=\left(2-\left(-1\right);2-\left(-1\right)\right)=\left(3;3\right)\)
b) Hình (H') có phương trình là:
\(y+3=\dfrac{3-\left(x+3\right)}{\left(x+3\right)+1}\) hay là \(y=\dfrac{-4x-12}{x+4}\)
Hình đối xứng với (H') qua gốc tọa độ có phương trình là:
\(-y=\dfrac{-4\left(-x\right)-12}{-x+4}\) hay là: \(y=\dfrac{4x-12}{-x+4}\)

Gọi \(M\left(x_0;y_0\right)\)là tiếp điểm. Ta có : \(y'=-3x^2+3\)
a) Vì tiếp tuyến vuông góc với đường thẳng \(x+y-1=0\Rightarrow y=-x+1\) nên ta có :
\(y'\left(x_0\right)=1\Leftrightarrow-3x^2_0+3=1\Leftrightarrow x_0=\pm\frac{\sqrt{6}}{3}\)
* \(x_0=\frac{\sqrt{6}}{3}\Rightarrow y_0=\frac{18+7\sqrt{6}}{9}\) nên ta có phương trình tiếp tuyến
\(y=\left(x-\frac{\sqrt{6}}{3}\right)+\frac{18+7\sqrt{6}}{9}=x+\frac{18+7\sqrt{6}}{9}\)
* \(x_0=-\frac{\sqrt{6}}{3}\Rightarrow y_0=\frac{18-7\sqrt{6}}{9}\) nên ta có phương trình tiếp tuyến
\(y=\left(x+\frac{\sqrt{6}}{3}\right)+\frac{18-7\sqrt{6}}{9}=x+\frac{18-7\sqrt{6}}{9}\)
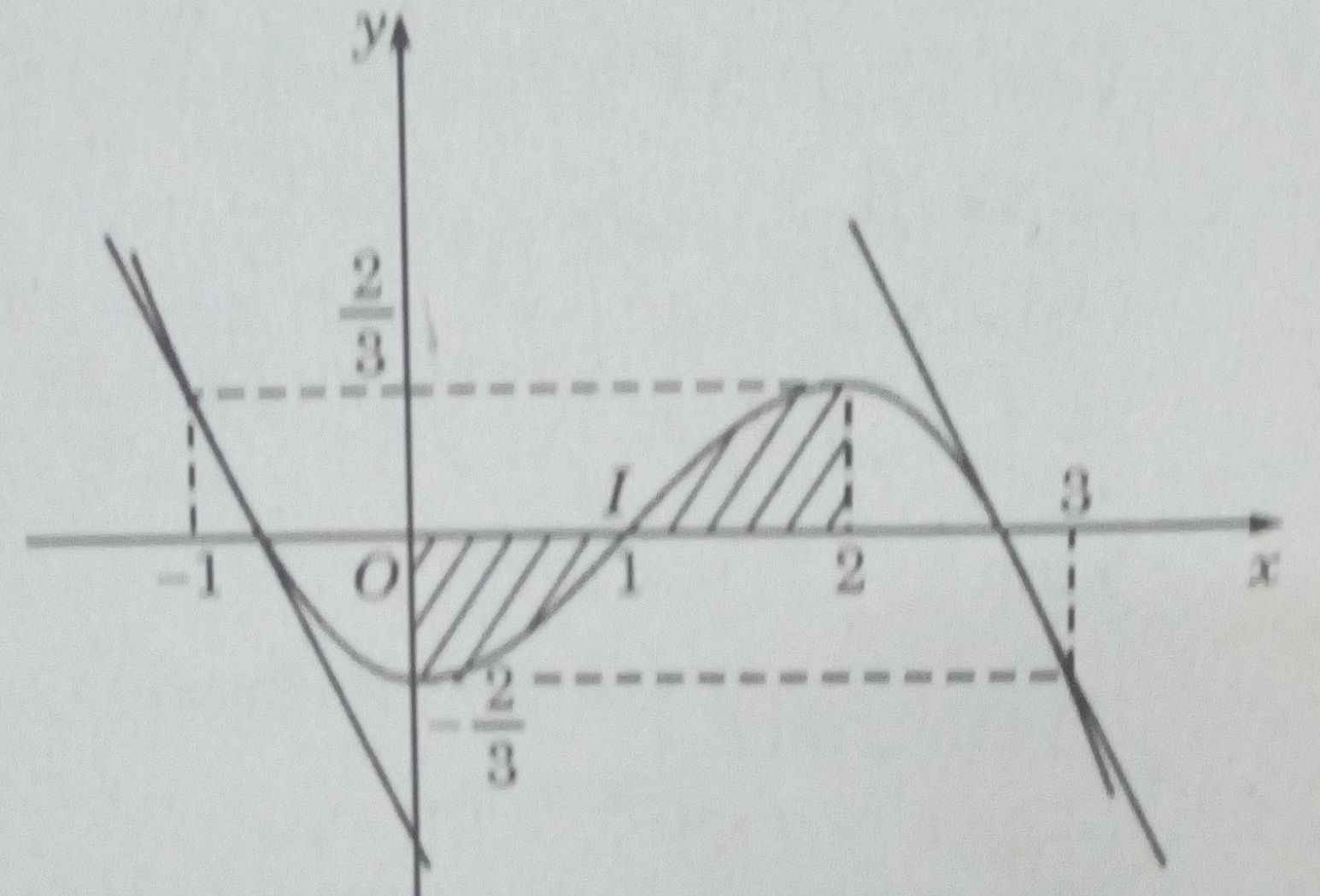
Vì \(\Delta\) tạo với \(\Delta'\) một góc bằng \(45^0\) nên \(\frac{\left|k-1\right|}{\sqrt{k^2+1}.\sqrt{2}}=\frac{\sqrt{2}}{2}\Leftrightarrow k=0\)
Ta có \(f'\left(x_0\right)=k\Leftrightarrow-3x^2_0+3=0\Leftrightarrow x_0=\pm1\)
* \(x_0=1\Rightarrow y_0=4\Rightarrow\Delta:y-4=0\)
* \(x_0=-1\Rightarrow y_0=-2\Rightarrow\Delta:y+2=0\)

a) Phương trình đường thẳng d có dạng: , với t ∈ R.
b) Đường thẳng d vuông góc với mặt phẳng (α): x + y - z + 5 = 0 nên có vectơ chỉ phương
(1 ; 1 ; -1) vì
là vectơ pháp tuyến của (α).
Do vậy phương trình tham số của d có dạng:
c) Vectơ (2 ; 3 ; 4) là vectơ chỉ phương của ∆. Vì d // ∆ nên
cùng là vectơ chỉ phương của d. Phương trình tham số của d có dạng:
d) Đường thẳng d đi qua hai điểm P(1 ; 2 ; 3) và Q(5 ; 4 ; 4) có vectơ chỉ phương
(4 ; 2 ; -1) nên phương trình tham số có dạng:


Vậy \(S=4\pi r^2=4\pi\left(\dfrac{a\sqrt{2}}{2}\right)^2=2\pi a^2\) và \(V=\dfrac{4}{3}\pi r^3=\dfrac{4}{3}\pi\left(\dfrac{a\sqrt{2}}{2}\right)^3=\dfrac{1}{3}\pi a^3\sqrt{2}\)





Chọn D
Có vô số phép tịnh tiến biến một đường thẳng d thành chính nó. Khi đó, vecto tịnh tiến có giá song song hoặc trùng với đường thẳng d.