
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


7.
\(V=\frac{\left(a\sqrt{2}\right)^3\pi.\sqrt{2}}{3}=\frac{4\pi a^3}{3}\)
8.
Mệnh đề B sai
Mệnh đề đúng là: \(lnx< 1\Rightarrow0< x< e\)
9.
\(\overline{z}=5-2i\Rightarrow z=5+2i\Rightarrow\left|z\right|=\sqrt{5^2+2^2}=\sqrt{29}\)
10.
\(\overrightarrow{NM}=\left(1;-3;-2\right)\) nên đường thẳng MN nhận \(\left(1;-3;-2\right)\) là 1 vtcp
Phương trình tham số: \(\left\{{}\begin{matrix}x=t\\y=1-3t\\z=3-2t\end{matrix}\right.\)
4.
\(V=3.4.5=60\)
5.
\(\left\{{}\begin{matrix}log_8a+2log_4b=5\\log_8b+2log_4a=7\end{matrix}\right.\)
\(\Rightarrow log_8a-log_8b-2\left(log_4a-log_4b\right)=-2\)
\(\Leftrightarrow log_8\frac{a}{b}-2log_4\frac{a}{b}=-2\)
\(\Leftrightarrow\frac{1}{3}log_2\frac{a}{b}-log_2\frac{a}{b}=-2\)
\(\Leftrightarrow-\frac{2}{3}log_2\frac{a}{b}=-2\)
\(\Leftrightarrow log_2\frac{a}{b}=3\)
\(\Rightarrow\frac{a}{b}=8\)
6.
\(log_{\frac{1}{5}}x=t\Rightarrow t^2-2t-3=0\Rightarrow\left[{}\begin{matrix}t=-1\\t=3\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}log_{\frac{1}{5}}x=-1\\log_{\frac{1}{5}}x=3\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=5\\x=\frac{1}{125}\end{matrix}\right.\)

Lời giải:
Đặt \(\log_yx=a,\log_xy=b\). Khi đó ta có:
\(\left\{\begin{matrix} a+b=\frac{10}{3}\\ ab=\log_xy.\log_yx=1\end{matrix}\right.\)
Áp dụng định lý Viete đảo thì \(a,b\) là nghiệm của PT:
\(x^2-\frac{10}{3}x+1=0\) . PT trên có hai nghiệm \(3,\frac{1}{3}\)
Giả sử \(a=\log_yx=3\) và \(b=\log_xy=\frac{1}{3}\)
\(\left\{\begin{matrix} \log_y\left(\frac{144}{y}\right)=3\\ \log_x\left(\frac{144}{x}\right)=\frac{1}{3} \end{matrix}\right.\Rightarrow \left\{\begin{matrix} x=24\sqrt{3}\\ y=2\sqrt{3}\end{matrix}\right.\)
\(\Rightarrow \frac{x+y}{2}=13\sqrt{3}\). Đáp án D

a) Đặt t = 13x > 0 ta được phương trình:
13t2 – t – 12 = 0 ⇔ (t – 1)(13t + 12) = 0
⇔ t = 1 ⇔ 13x = 1 ⇔ x = 0
b)
Chia cả hai vế phương trình cho 9x ta được phương trình tương đương
(1+(23)x)(1+3.(23)x)=8.(23)x(1+(23)x)(1+3.(23)x)=8.(23)x
Đặt t=(23)xt=(23)x (t > 0) , ta được phương trình:
(1 + t)(1 + 3t) = 8t ⇔ 3t2 – 4t + 1 = 0 ⇔ t∈{13,1}t∈{13,1}
Với t=13t=13 ta được nghiệm x=log2313x=log2313
Với t = 1 ta được nghiệm x = 0
c) Điều kiện: x > 2
Vì nên phương trình đã cho tương đương với:
[log3(x−2)=0log5x=1⇔[x=3x=5[log3(x−2)=0log5x=1⇔[x=3x=5
d) Điều kiện: x > 0
log22x – 5log2x + 6 = 0
⇔(log2x – 2)(log2x – 3) = 0
⇔ x ∈ {4, 8}




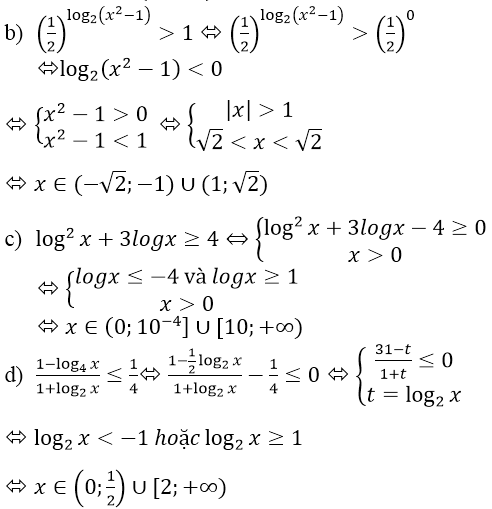


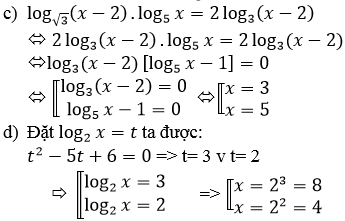
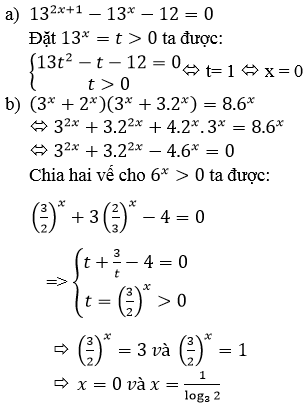
Đáp án B