Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Phương pháp:
+) Đường thẳng x = a được gọi là TCĐ của đồ thị hàm số

Đồ thị hàm số chỉ có đúng 2 đường tiệm cận ⇔ đồ thị hàm số có đúng 1 tiệm cận đứng.

Như vậy có: 2008 giá trị m thỏa mãn bài toán.

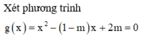
Đồ thị hàm số đã cho có 2 đường tiệm cận đứng ⇔ phương trình g(x) có 2 nghiệm phân biệt
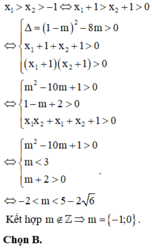

Đáp án C
Yêu cầu bài toán ⇔ x 2 - ( 1 - m ) x + 2 m = 0 có 2 nghiệm phân biệt lớn hơn hoặc bằng -1
Khi và chỉ khi ∆ > 0 x 1 + x 2 + 2 ≥ 0 x 1 + 1 x 2 + 1 ≥ 0 ⇔ 1 - m 2 - 4 . 2 m > 0 1 - m + 2 ≥ 0 2 m + 2 - m + 1 ≥ 0 ⇔ - 2 ≤ m ≤ 5 - 2 6 .

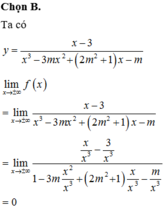
Nên y = 0 là tiệm ngang của đồ thị hàm số.
Vậy để đồ thị hàm số có 4 đường tiệm cận thì đồ thị hàm số phải có 3 đường tiệm cận đứng.
Hay phương trình
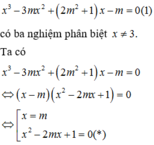
Để phương trình (1) có ba nghiệm phân biệt khác 3 thì m khác 3 và phương trình (*) có hai nghiệm phân biệt khác m và khác 3.
Do đó
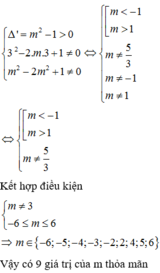

hoành độ giao điểm là nghiệm của pt
\(x^3-3mx^2+3\left(2m-1\right)x+1=2mx-4m+3\Leftrightarrow x^3-3mx^2+4mx-3x-2+4m=0\Leftrightarrow x^3-3x-2-m\left(3x^2-4x+4\right)=0\)
giải hệ pt ta có \(C_m\) luôn đi qua điểm A là nghiệm của hệ pt sau
\(\begin{cases}3x^2-4x+4=0\\x^3-3x-2=0\end{cases}\)
ta đc điều phải cm

*x2+bx+c=0
\(\Delta=b^2-4c=b^2-4.\left(2b-4\right)=b^2-8b+16=\left(b-4\right)^2\)=>\(\sqrt{\Delta}=\left|b-4\right|\)
Với (b-4)2=0 =>b=4 =>c=4
PT có 1 nghiệm kép: \(x_1=x_2=-2\)
Với\(\Delta=\) (b-4)2>0,PT có 2 nghiệm pb: \(x_1=\frac{-b+\left|b-4\right|}{2};x_2=\frac{-b-\left|b-4\right|}{2}\)
Với b>4 thì: \(x_1=-2;x_2=\frac{-2b+4}{2}=-b+2\)
Với b<0 thì: x1=-b+2 ; x2=-2
Vậy khi c=2b-4 và b tùy ý thì PT: x2+bx+c=0 luôn có 1 nghiệm nguyên là -2

Đáp án C
Phương pháp: Để đồ thị hàm số có tiệm cận đứng x = x 0 thì x 0 là nghiệm của phương trình mẫu mà không là nghiệm của phương trình tử.
Cách giải:
ĐK: x ≥ - 1 và x 2 - ( 1 - m ) x + 2 m > 0
Xét phương trình 1 + x + 1 = 0 vô nghiệm
Xét phương trình x 2 - ( 1 - m ) x + 2 m = 0 (*). Để đồ thị hàmsố có hai TCĐ thì phương trình có 2 nghiệm phân biệt thỏa mãn ĐK x ≥ - 1
![]()

Khi đó gọi hai nghiệm của phương trình là x 1 > x 2 ta có:
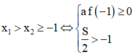
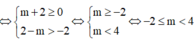
Kết hợp điều kiện ta có: 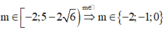
Thử lại:
Với ![]()
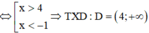
Khi đó hàm số có dạng 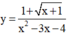 có 1 tiệm cận đứng x = 4 => Loại
có 1 tiệm cận đứng x = 4 => Loại
Với 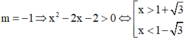
![]()
Khi đó hàm số có dạng  có 2 tiệm cận đứng x = 1±
3
=> TM
có 2 tiệm cận đứng x = 1±
3
=> TM
Khi 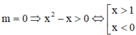
![]()
Khi đó hàm số có dạng 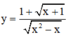 có 2 tiệm cận đứng x = 0; x = 1 => TM
có 2 tiệm cận đứng x = 0; x = 1 => TM
Vậy ![]()


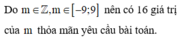
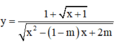 có hai tiệm cận đứng?
có hai tiệm cận đứng?
Chọn D.
Phương pháp:
Khi đó, để có hai tiệm cận đứng thì (1) có 2 nghiệm phân biệt