
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

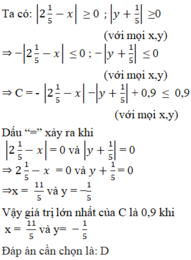

a) (3x + 1)3 = -27
=> (3x + 1)3 = (-3)3
=> 3x + 1 = -3
=> 3x = -3 - 1
=> 3x = -4
=> x = -4/3
b) |2,5 - x| = 1,3
=> \(\orbr{\begin{cases}2,5-x=1,3\\2,5-x=-1,3\end{cases}}\)
=> \(\orbr{\begin{cases}x=1,2\\x=3,8\end{cases}}\)
c) 0,5 - |x - 3,5| = 0
=> |x - 3,5| = 0,5
=> \(\orbr{\begin{cases}x-3,5=0,5\\x-3,5=-0,5\end{cases}}\)
=> \(\orbr{\begin{cases}x=4\\x=3\end{cases}}\)
d) Ta có: |x + 2| \(\ge\)0 \(\forall\)x
|x2 - 4| \(\ge\)0 \(\forall\)x
=> |x + 2| + |x2 - 4| \(\ge\)0 \(\forall\)x
Dấu "=" xảy ra khi: x + 2 + x2 - 4 = 0
=> x2 + x - 2 = 0
=> x2 + 2x - x - 2 = 0
=> x(x + 2) - (x + 2) = 0
=> (x - 1)(x + 2) = 0
=> \(\orbr{\begin{cases}x-1=0\\x+2=0\end{cases}}\)
=> \(\orbr{\begin{cases}x=1\left(l\right)\\x=-2\end{cases}}\)
\(a,\left(3x+1\right)^3=-27\)
\(\Leftrightarrow3x+1=\sqrt[3]{-27}\)
\(\Leftrightarrow3x+1=-3\)
\(\Leftrightarrow3x=-4\Leftrightarrow x=-\frac{4}{3}\)
b, \(|2,5-x|=1,3\)
\(Th1:2,5-x=1,3\Leftrightarrow x=2,5-1,3\)
\(\Leftrightarrow x=1,2\)
\(Th2:x-2,5=1,3\Leftrightarrow x=1,3+2,5\)
\(\Rightarrow x=3,8\)
c, \(0,5-|x-3,5|=0\)
\(th1:0,5-x+3,5=0\Leftrightarrow4-x=0\)
\(\Rightarrow x=4\)
\(Th2:0,5+x-3,5=0\Leftrightarrow x-3=0\)
\(\Rightarrow x=3\)
d, \(|x+2|+|x^2-4|=0\)
\(x+2=0\Leftrightarrow x=-2\)

|3x - 1| = 32
=> |3x - 1| = 9
=> 3x - 1 = 9 hoặc 3x - 1 = -9
=> 3x = 10 hoặc 3x = -8
=> x = 10/3 hoặc x = -8/3
Mà x < 0
=> x = -8/3


Áp dụng bđt \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\) ta có:
\(\left|2x-2\right|+\left|2x-6\right|=\left|2x-2\right|+\left|6-2x\right|\ge\left|2x-2+6-2x\right|=\left|4\right|=4\)
Do đó, |2x - 2| + |2x - 6| < 4 là vô lý
Vậy không tồn tại giá trị x nguyên thỏa mãn đề bài

