Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

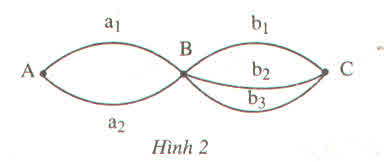
\(\left\{a_1b_1;a_1b_2;a_1b_3;a_2b_1;a_2b_2;a_2b_3\right\}\)

a)
\(175\cdot19+38\cdot175+43\cdot175\\ =175\cdot19+175\cdot38+175\cdot43\\ =175\cdot\left(19+38+43\right)\\ =175\cdot100\\ =17500\)
b)
\(125\cdot75+125\cdot13-80\cdot125\\ =125\cdot75+125\cdot13-125\cdot80\\ =125\cdot\left(75+13-80\right)\\ =125\cdot10\\ =125\cdot8\\ =1000\)
a, 175. 19 + 38. 175 + 43. 175
= 175. 19 + 175. 38 + 175. 43
= 175.(19 + 38 + 43)
= 175. 100
= 17500

Bài 1:
e; \(\dfrac{10}{21}\) - \(\dfrac{3}{8}\) : \(\dfrac{15}{4}\)
= \(\dfrac{10}{21}\) - \(\dfrac{3}{8}\) x \(\dfrac{4}{15}\)
= \(\dfrac{10}{21}\) - \(\dfrac{1}{10}\)
= \(\dfrac{100}{210}\) - \(\dfrac{21}{210}\)
= \(\dfrac{79}{210}\)
f; (\(\dfrac{2}{3}\) + \(\dfrac{3}{4}\)).(\(\dfrac{5}{7}\) + \(\dfrac{5}{14}\))
= (\(\dfrac{8}{12}\) + \(\dfrac{9}{12}\)).(\(\dfrac{10}{14}\) + \(\dfrac{5}{14}\))
= \(\dfrac{17}{12}\).\(\dfrac{15}{14}\)
= \(\dfrac{85}{56}\)

a) Có 18 học sinh đi đến trường bằng xe đạp.
b) Lớp 6A có 45 học sinh.
c) Tỉ số phần trăm học sinh đi bộ đến trường là:
(9 : 45) . 100 = 20%

Ta đặt tên các đỉnh như hình vẽ sau:
ABCDEFGHIJKMNOPQRSTU
Ta có nhận xét sau:
1) Số đường đi hợp lệ từ A đến các đỉnh nằm trên cạnh phía trên của lưới ô vuông C, D, E, F luôn là 1 (ví dụ từ A đến D chỉ có đường duy nhất là A-->C-->D)
2) Số đường đi hợp lệ từ A đến các đỉnh nằm trên cạnh bên trái của lưới ô vuông G, M, R cũng là 1 (Ví dụ từ A đến R chỉ có đúng 1 đường duy nhất là A-->G-->M-->R)
Ta ghi số cách đi hợp lệ từ A đến một đỉnh bằng số màu đỏ như hình vẽ dưới.
ABCDEFGHIJKMNOPQRSTU11111111
3) Ta tính số đường đi từ A đến các đỉnh còn lại theo qui tắc đệ qui (hoặc qui nạp) như sau:
- Đỉnh H: có 3 cách đi: A-->C-->H ; A-->H ; A -->G-->H
- Đỉnh I: Các đường đi từ A đến I được phân thành 3 loại:
+ đi qua đoạn DI: từ là từ A đến D rồi đến DI
+ đi qua đoạn CI: từ A đến C rồi đoạn CI
+ đi qua đoạn HI: từ A đến H rồi đoạn HI
Như vậy
[số đường đi từ A đến I] = [số đường đi từ A đến D] + [số đường đi từ A đến C] + [số đường đi từ A đến H]
= 1 + 1 + 3
= 5
(xem hình vẽ minh hoạ bên dưới)
ABCDEFGHIJKMNOPQRSTU1111111135
- Đỉnh J: Tương tự như cách tính đỉnh I:
[số đường đi từ A đến J] = [số đường đi từ A đến E] + [số đường đi từ A đến D] + [số đường đi từ A đến I]
= 1 + 1 + 5
= 7
(xem hình vẽ minh hoạ bên dưới)
ABCDEFGHIJKMNOPQRSTU11111111357
Cứ lặp lại tính như vậy cho các đỉnh còn lại. Ta sẽ điền được số đường đi hợp lệ từ A đến các đỉnh khác nhau như hình dưới đây:
AB111111113579513254172563129
Số đường đi hợp lệ từ A đến B là 129 đường.

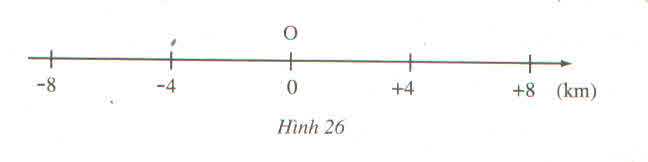
gọi vị trí người ₫ó là A
a\()\) A là v.t\(=\) 4.2
A là 8 km
=> O cách A = 8km
b) A là v.t = -4 .2 = -8 km
=> O cách A = 8km
c) A là ( -4 ).2=-8km
=> O cách A 8km
d ) A là ( -4 )(-2)=8km
=> O cách A là 8 km

Olm chào em, khi em muốn đổi quà thì em đổi qua hệ thống. Olm không có chương trình nào là đổi 50 xu lấy quà có giá trị lớn cả. Với lại đổi quà thì phải đổi qua hệ thống chứ sao lại chuyển cho một người vô danh trên Olm được. Em cho cô xin link để cô khóa tài khoản của người này lại. Cảm ơn em

Sau 30 phút Hùng đi được quãng đường là :
\(\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{2}{9}-\dfrac{29}{36}\) (quãng đường).
Đ/s : \(\dfrac{29}{36}\) quãng đường
Sau 30 phút Hùng đi được số phàn quãng đường là :
\(\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{2}{9}=\dfrac{29}{36}\)( quãng đường )
Vậy sau 30 phút Hùng đi được \(\dfrac{29}{36}\)quãng đường

Câu 8:
a:Sửa đề: \(4+4^2+\cdots+4^{2025}\)
Ta có: \(4+4^2+\cdots+4^{2025}\)
\(=\left(4+4^2+4^3\right)+\left(4^4+4^5+4^6\right)+\cdots+\left(4^{2023}+4^{2024}+4^{2025}\right)\)
\(=4\left(1+4+4^2\right)+4^4\left(1+4+4^2\right)+\cdots+4^{2023}\left(1+4+4^2\right)\)
\(=21\left(4+4^4+\cdots+4^{2023}\right)\) ⋮21
b: \(5+5^2+5^3+5^4+\cdots+5^{2024}\)
\(=\left(5+5^2\right)+\left(5^3+5^4\right)+\cdots+\left(5^{2023}+5^{2024}\right)\)
\(=\left(5+5^2\right)+5^2\left(5+5^2\right)+\cdots+5^{2022}\left(5+5^2\right)\)
\(=30\left(1+5^2+\cdots+5^{2022}\right)\) ⋮30
Câu 7:
a: \(A=2+2^2+2^3+\cdots+2^{99}\)
=>\(2A=2^2+2^3+\cdots+2^{100}\)
=>\(2A-A=2^2+2^3+\cdots+2^{100}-2-2^2-\cdots-2^{99}\)
=>\(A=2^{100}-2\)
b: \(B=1-7+7^2-7^3+\cdots+7^{48}-7^{49}\)
=>\(7B=7-7^2+7^3-7^4+\cdots+7^{49}-7^{50}\)
=>\(7B+B=7-7^2+7^3-7^4+\cdots+7^{49}-7^{50}+1-7+7^2-7^3+\cdots+7^{48}-7^{49}\)
=>\(8B=-7^{50}+1\)
=>\(B=\frac{-7^{50}+1}{8}\)
Câu 7
a) \(A=2+2^2+2^3+\ldots+2^{99}\).
Đây là cấp số nhân từ \(2^{1}\) đến \(2^{99}\). Tổng:
\(A = \sum_{k = 1}^{99} 2^{k} = \frac{2 \left(\right. 2^{99} - 1 \left.\right)}{2 - 1} = 2 \left(\right. 2^{99} - 1 \left.\right) = 2^{100} - 2.\)
b) \(B=1-7+7^2-7^3+\ldots+7^{48}-7^{49}\).
Đây là tổng các \(7^{k}\) với dấu luân phiên, tức là tổng cấp số nhân với tỉ số \(r = - 7\), từ \(k = 0\) đến \(k = 49\):
\(B = \sum_{k = 0}^{49} \left(\right. - 1 \left.\right)^{k} 7^{k} = \sum_{k = 0}^{49} \left(\right. - 7 \left.\right)^{k} = \frac{1 - \left(\right. - 7 \left.\right)^{50}}{1 - \left(\right. - 7 \left.\right)} = \frac{1 - 7^{50}}{8} .\)
(Đó là dạng rút gọn chính xác.)
Câu 8
a) Dạng đề: \(1+4+4^2+4^3+\ldots+4^{2025}\) chia hết cho \(21\) ?
Hãy xét chu kỳ của \(4^{n}\) theo mod \(21\). Ta có
\(4^{1} \equiv 4 , 4^{2} \equiv 16 , 4^{3} = 64 \equiv 1 \left(\right. m o d 21 \left.\right) ,\)
vậy \(4^{3} \equiv 1 \left(\right. m o d 21 \left.\right)\) — nghĩa là dãy lũy thừa của 4 theo mod 21 có chu kỳ 3. Tổng mỗi nhóm ba số liên tiếp
\(4^{0} + 4^{1} + 4^{2} = 1 + 4 + 16 = 21 \equiv 0 \left(\right. m o d 21 \left.\right) .\)
Tập các số từ \(4^{0}\) đến \(4^{2025}\) có \(2026\) số. Vì \(2026 = 3 \cdot 675 + 1\), nên ta có \(675\) nhóm 3 (mỗi nhóm tổng chia hết cho 21) và dư một số là \(4^{2025}\). Do \(2025\) chia hết cho \(3\), ta có \(4^{2025} \equiv 4^{0} \equiv 1 \left(\right. m o d 21 \left.\right)\).
Vậy tổng toàn bộ hợp lại
\(\equiv 675 \cdot 0 + 1 \equiv 1 \left(\right. m o d 21 \left.\right) ,\)
không chia hết cho \(21\).
Kết luận: Như đề bài viết (tới \(4^{2025}\)), tổng không chia hết cho \(21\).
(Có lẽ đề thực tế muốn mũ cuối là \(2024\) thay vì \(2025\); khi mũ cuối là \(2024\) thì có \(2025\) số, tức \(2025 = 3 \cdot 675\) nhóm đầy đủ nên tổng sẽ chia hết cho \(21\).)
b) Dạng đề: \(5 + 5^{2} + 5^{3} + \hdots + 5^{2024}\) chia hết cho \(30\) ?
Gọi \(S = \sum_{k = 1}^{2024} 5^{k}\). Ta kiểm tra chia hết cho \(2 , 3 , 5\) (vì \(30 = 2 \cdot 3 \cdot 5\)):
- Chia cho \(5\): mỗi \(5^{k}\) có \(5\) là thừa số, nên tổng \(S\) chia hết cho \(5\).
- Chia cho \(2\): với modulo \(2\), \(5 \equiv 1\). Do đó mỗi \(5^{k} \equiv 1 \left(\right. m o d 2 \left.\right)\). Có \(2024\) số nên tổng theo modulo \(2\) là \(2024 \cdot 1 \equiv 0 \left(\right. m o d 2 \left.\right)\). Vậy chia hết cho \(2\).
- Chia cho \(3\): \(5 \equiv 2 \left(\right. m o d 3 \left.\right)\). Lũy thừa luân phiên: \(5^{1} \equiv 2 , \textrm{ }\textrm{ } 5^{2} \equiv 1 , \textrm{ }\textrm{ } 5^{3} \equiv 2 , \textrm{ }\textrm{ } 5^{4} \equiv 1 , \ldots\) (chu kỳ 2). Vì \(2024\) là số chẵn, các cặp \(\left(\right. 5^{2 m - 1} + 5^{2 m} \left.\right) \equiv 2 + 1 \equiv 0 \left(\right. m o d 3 \left.\right)\). Do đó tổng chia hết cho \(3\).
Từ đó \(S\) chia hết cho \(2 , 3 , 5\) đồng thời, nên chia hết cho \(30\).

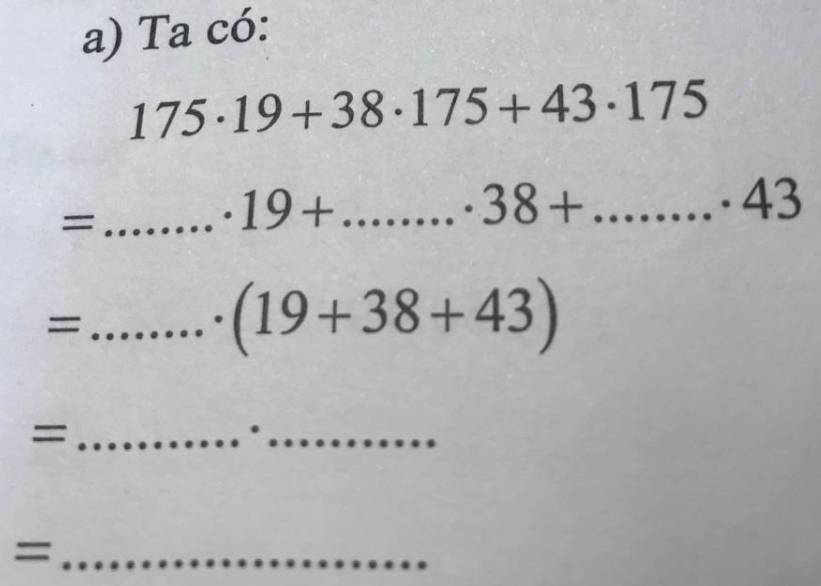
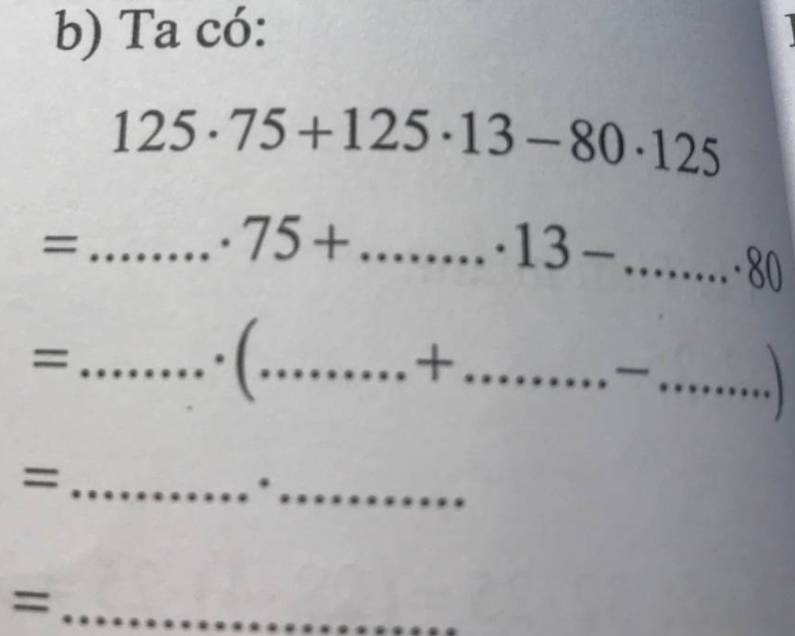





5