Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) tham khảo trên trang này:
https://lazi.vn/edu/exercise/748977/chung-minh-rang-neu-2-goc-xoy-va-goc-xoy-cung-nhon-hoac-cung-tu-co-ox-vuong-goc-voi-ox-va-oy-vuong-goc-voi-oy-thi-goc-xoy-goc-xoy#:~:text=B%C3%A0i%20t%E1%BA%ADp-,Ch%E1%BB%A9ng%20minh%20r%E1%BA%B1ng%20%3A%20N%E1%BA%BFu%202%20g%C3%B3c%20xOy%20v%C3%A0%20g%C3%B3c%20x%27O%27y%27%20c%C3%B9ng%20nh%E1%BB%8Dn%20ho%E1%BA%B7c%20c%C3%B9ng%20t%C3%B9%20c%C3%B3%20Ox%20vu%C3%B4ng%20g%C3%B3c%20v%E1%BB%9Bi%20Ox%27%20v%C3%A0%20Oy%20vu%C3%B4ng%20g%C3%B3c%20v%E1%BB%9Bi%20Oy%27%20th%C3%AC%20g%C3%B3c%20xOy%20%3D%20g%C3%B3c%20x%27O%27y%27,-Lan%20Nguy%E1%BB%85n%20%7C%20%20Chat

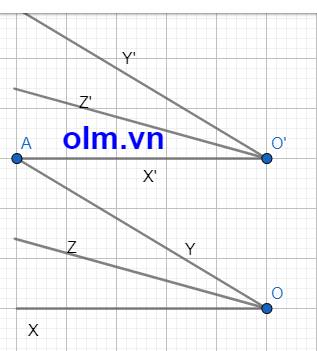
a,Kéo dài OY cắt O'X' tại A ta có:
\(\widehat{XOY}\) = \(\widehat{XOA}\) = \(\widehat{OAO'}\) (so le trong) (1)
\(\widehat{Y'O'X'}\) = \(\widehat{Y'O'A}\) = \(\widehat{OAO'}\) (so le trong) (2)
Kết hợp (1) Và (2) ta có:
\(\widehat{XOY=}\) \(\widehat{X'O'Y'}\) (đpcm)
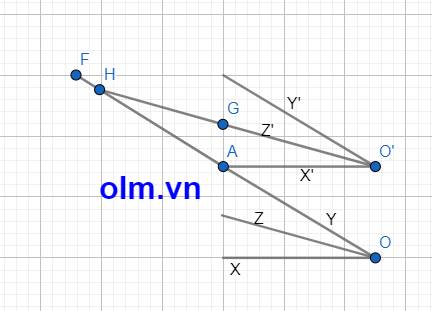
b, Kéo dài OY cắt O'Z' tại H
\(\widehat{ZOA}\) = \(\dfrac{1}{2}\) \(\widehat{XOY}\) (vì OZ là phân giác của góc XOY
\(\widehat{HO'A}\) = \(\dfrac{1}{2}\) \(\widehat{X'O'Y'}\) (vì OY là phân giác của góc X'O'Y')
Mặt khác ta có \(\widehat{OAO'}\) = \(\widehat{HO'A}\) + \(\widehat{AHO'}\) (góc ngoài tam giác bằng tổng hai góc trong không kề với nó)
\(\widehat{HO'A}\) = \(\dfrac{1}{2}\) \(\widehat{OAO'}\) ⇒ \(\widehat{AHO'}\) = \(\dfrac{1}{2}\) \(\widehat{OAO'}\) = \(\dfrac{1}{2}\) \(\widehat{XOY}\)
⇒ \(\widehat{ZOA}\) = \(\widehat{AHO'}\) (hai góc này ở vị trí so le trong)
⇒ OZ // O'Z' (đpcm)



1) Ta có: Oz nằm giữa tia Ox và Oy
\(\Rightarrow\widehat{xOz}=\widehat{xOy}-\widehat{yOz}=120^0-30^0=90^0\)
=> Oz⊥Ox
2) Ta có: Ox' là tia đối của tia Ox
\(\Rightarrow\widehat{x'Oy}=180^0-\widehat{xOy}=180^0-120^0=60^0\)(2 góc kề bù)
Ta có: Ox' là tia đối của tia Ox, Oy' là tia đối của tia Oy
\(\widehat{\Rightarrow x'Oy'}=\widehat{xOy}=120^0\)(2 góc đối đỉnh)
1: Trên cùng một nửa mặt phẳng bờ chứa tia Oy, ta có: \(\widehat{yOz}< \widehat{yOx}\)
nên tia Oz nằm giữa hai tia Ox và Oy
Suy ra: \(\widehat{xOz}+\widehat{yOz}=\widehat{xOy}\)
\(\Leftrightarrow\widehat{xOz}=90^0\)
hay Ox\(\perp\)Oz