Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Gọi A là tập hợp tất cả cách sắp xếp, ![]() là tập hợp các cách xếp mà chữ cái T đứng cạnh nhau,
là tập hợp các cách xếp mà chữ cái T đứng cạnh nhau, ![]() là tập hợp các cách xếp mà chữ cái D đứng cạnh nhau.
là tập hợp các cách xếp mà chữ cái D đứng cạnh nhau.
Ta có số phần tử của tập hợp A là ![]() (do 2 chữ T như nhau, 2 chữ C như nhau
(do 2 chữ T như nhau, 2 chữ C như nhau
nên khi hoán vị vẫn tính là 1).
Số phân tử của tập hợp ![]() lần lượt là
lần lượt là ![]() (ta coi 2 chữ T đứng cạnh nhau là 1 chữ, 2 chữ C đứng cạnh nhau là 1 chữ).
(ta coi 2 chữ T đứng cạnh nhau là 1 chữ, 2 chữ C đứng cạnh nhau là 1 chữ).
Số cách sắp xếp mà vừa có T đứng cạnh nhau, c đứng cạnh nhau là ![]()
Vậy số cách sắp xếp cần tính là
![]() .
.

a) Để đi từ A đến D mà qua B và C chỉ một lần, phải thực hiện liên tiếp ba hành động sau đây:
Hành động 1: Đi từ A đến B. Có 4 cách để thực hiện hành động này.
Hành động 2: Đi từ B đến C. Có 2 cách để thực hiện hành động này.
Hành động 3: Đi từ C đến D. Có 3 cách để thực hiện hành động này.
Theo quy tắc nhân suy ra số các cách để đi từ A đến D mà qua B và C chỉ một lần là 4 . 2 . 3 = 24 (cách).
b) ĐS: Số các cách để đi từ A đến D (mà qua B và C chỉ một lần), rồi quay lại A (mà qua C và B chỉ một lần) là:
(4 . 2 . 3) . (3 . 2 . 4) = 242 = 576 (cách).


1.
\(\lim\left(\sqrt{9^n-2.3^n}-3^n+\dfrac{1}{2021}\right)\)
\(=\lim\left(\dfrac{\left(\sqrt{9^n-2.3^n}-3^n\right)\left(\sqrt{9^n-2.3^n}+3^n\right)}{\sqrt{9^n-2.3^n}+3^n}+\dfrac{1}{2021}\right)\)
\(=\lim\left(\dfrac{-2.3^n}{\sqrt{9^n-2.3^n}+3^n}+\dfrac{1}{2021}\right)\)
\(=\lim\left(\dfrac{-2.3^n}{3^n\left(\sqrt{1-\dfrac{2}{3^n}}+1\right)}+\dfrac{1}{2021}\right)\)
\(=\lim\left(\dfrac{-2}{\sqrt{1-\dfrac{2}{3^n}}+1}+\dfrac{1}{2021}\right)\)
\(=\dfrac{-2}{1+1}+\dfrac{1}{2021}=-\dfrac{2020}{2021}\)
2.
\(AP=4PB=4\left(AB-AP\right)=4AB-4AP\)
\(\Rightarrow5AP=4AB\Rightarrow AP=\dfrac{4}{5}AB\)
\(\Rightarrow\overrightarrow{AP}=\dfrac{4}{5}\overrightarrow{AB}\)
\(CD=5CQ=5\left(CD-DQ\right)\Rightarrow5DQ=4CD\Rightarrow DQ=\dfrac{4}{5}CD\)
\(\Rightarrow\overrightarrow{DQ}=-\dfrac{4}{5}\overrightarrow{CD}\)
Ta có:
\(\overrightarrow{PQ}=\overrightarrow{PA}+\overrightarrow{AD}+\overrightarrow{DQ}=-\dfrac{4}{5}\overrightarrow{AB}+\overrightarrow{AD}-\dfrac{4}{5}\overrightarrow{CD}\)
\(=-\dfrac{4}{5}\left(\overrightarrow{AD}+\overrightarrow{DB}\right)+\overrightarrow{AD}-\dfrac{4}{5}\overrightarrow{CD}=-\dfrac{4}{5}\overrightarrow{AD}-\dfrac{4}{5}\overrightarrow{DB}+\overrightarrow{AD}-\dfrac{4}{5}\overrightarrow{CD}\)
\(=\dfrac{1}{5}\overrightarrow{AD}-\dfrac{4}{5}\left(\overrightarrow{CD}+\overrightarrow{DB}\right)=\dfrac{1}{5}\overrightarrow{AD}-\dfrac{4}{5}\overrightarrow{CB}\)
\(=\dfrac{1}{5}\overrightarrow{AD}+\dfrac{4}{5}\overrightarrow{BC}\)
Mà \(\overrightarrow{AD};\overrightarrow{BC}\) không cùng phương\(\Rightarrow\overrightarrow{AD};\overrightarrow{BC};\overrightarrow{PQ}\) đồng phẳng


1.
\(u_{n+1}=4u_n+3.4^n\)
\(\Leftrightarrow u_{n+1}-\dfrac{3}{4}\left(n+1\right).4^{n+1}=4\left[u_n-\dfrac{3}{4}n.4^n\right]\)
Đặt \(u_n-\dfrac{3}{4}n.4^n=v_n\Rightarrow\left\{{}\begin{matrix}v_1=2-\dfrac{3}{4}.4=-1\\v_{n+1}=4v_n\end{matrix}\right.\)
\(\Rightarrow v_n=-1.4^{n-1}\)
\(\Rightarrow u_n=\dfrac{3}{4}n.4^n-4^{n-1}=\left(3n-1\right)4^{n-1}\)
2.
\(a_n=\dfrac{a_{n-1}}{2n.a_{n-1}+1}\Rightarrow\dfrac{1}{a_n}=2n+\dfrac{1}{a_{n-1}}\)
\(\Leftrightarrow\dfrac{1}{a_n}-n^2-n=\dfrac{1}{a_{n-1}}-\left(n-1\right)^2-\left(n-1\right)\)
Đặt \(\dfrac{1}{a_n}-n^2-n=b_n\Rightarrow\left\{{}\begin{matrix}b_1=2-1-1=0\\b_n=b_{n-1}=...=b_1=0\end{matrix}\right.\)
\(\Rightarrow\dfrac{1}{a_n}=n^2+n\Rightarrow a_n=\dfrac{1}{n^2+n}\)

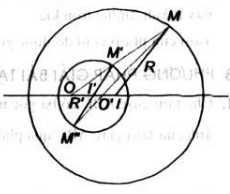
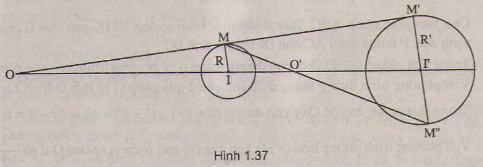
Lấy điểm M thuộc đường tròn (I). Qua I' kẻ đường thẳng song song với IM, đường thẳng này cắt đường tròn (I') tại M' và M''. Hai đường thẳng MM' và MM'' cắt đường thẳng II' theo thứ tự O và O'. Khi đó, O và O' là các tâm vị tự cần tìm
Vì hai đường tròn đã cho có bán kính khác nhau nên chúng có hai tâm vị tự là O và O', xác định trong từng trường hợp như sau ( xem hình vẽ):
a) Trường hợp 1:
b) Trường hợp 2:
c) Trường hợp 3:
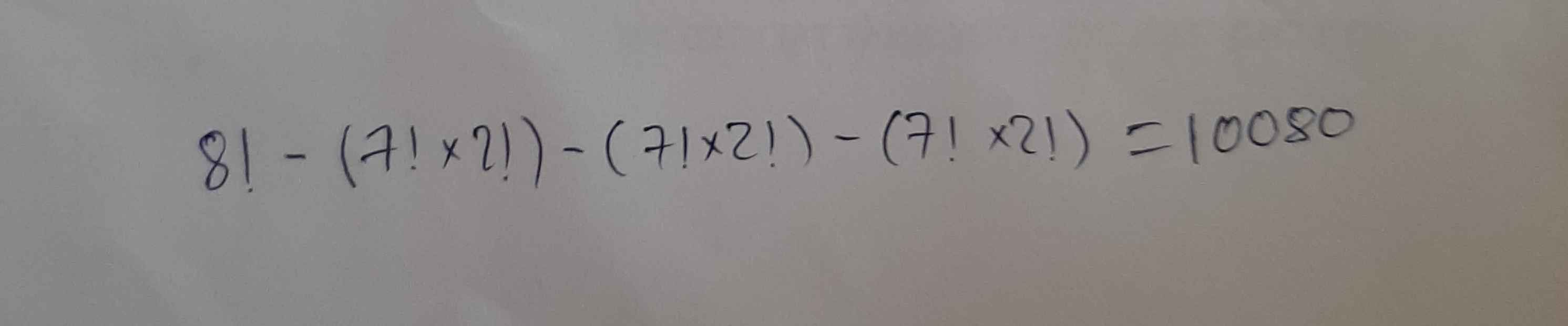







Cho mình hỏi, sao cách này lại sai. Ý tưởng của mình là 8 số lặp trừ đi cặp số đứng gần
Chỉ ra cách sai rồi giải theo ý tưởng hóa vị được không mn ới, help me