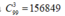Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Giả sử 100 đồ vật được xếp thành hàng ngang, giữa chúng có 99 khoảng trống. Đặt một cách bất kì 3 vạch vào 99 khoảng trống đó, ta được một cách chia 100 đồ vật ra thành 4 phần để lần lượt gán cho 4 người. Khi đó mỗi người được ít nhất 1 đồ vật và tổng đồ vật của 2 người bằng 100, thỏa mãn yêu cầu bài toán.
Vậy số cách chia đồ vật thỏa mãn là C 99 3 = 156849

Đáp án B
Vì số cách chia không tính đến thứ tự các vật nên cách chia đồ vật được tính theo công thức tổ hợp C 8 2 . C 6 3 . C 3 3 = C 8 2 . C 6 3

Đáp án A
Có C 3 1 cách chọn người được 2 đồ vật. Có C 8 2 cách chọn đồ vật đưa cho người đó
Có C 6 3 cách đưa đồ vật cho 2 người còn lại mà mỗi người 3 đồ vật.
Vậy có C 3 1 C 8 2 C 6 3 = 1680 cách chọn.

Lời giải: 17 phút
Phương án đầu tiên mà hầu hết mọi người nghĩ đến là để người đàn ông nhanh nhất đi trước và người thứ nhất sẽ lần lượt quay lại dẫn đường cho 3 người còn lại qua cầu.
Tổng cộng sẽ mất: 10 phút (D) + 1 phút (A quay lại) + 7 phút (A+C) + 1 phút (A quay lại) + 2 (A+B) = 21 phút. Nếu vậy thì bài toán quá dễ rồi.
Để giảm thời gian, chúng ta nên tìm cách cho D và C đi với nhau. Nếu họ đi qua cầu đầu tiên, họ sẽ cần một người quay lại đón người khác.
Như thế thì quá mất thời gian. Thử để A đi cùng B và để A đợi ở phía kia cây cầu. Sau khi B quay lại, C và D sẽ qua cầu và đưa đuốc cho A đón B sang.
A và B qua cầu => 2 phút
B quay lại => 2 phút
C và D qua cầu => 10 phút
A quay lại => 1 phút
A và B qua cầu => 2 phút
Tổng là: 2 + 2 + 10 + 1 + 2 = 17 phút
A và B qua cầu: 2 phút
B quay lại: 2 phút
C và D qua cầu: 10 phút
A quay lại: 1 phút
A và B qua cầu: 2 phút
Tổng thời gian: 17 phút

50 người đầu tiên nói đúng, 50 người cuối cùng nói sai. - Nếu ng1 SAI => phủ định của "Ít nhất một người nói sai" => không có ai SAI => vô lý (vì ng1 đã nói SAI) => ng1 nói ĐÚNG, Ít nhất một người phát biểu SAI - Nếu ng100 nói ĐÚNG => Ít nhất 100 người nói sai => cả 100ng nói SAI => vô lý (vì ng1 nói ĐÚNG) => ng100 nói SAI, số người nói đúng nhỏ hơn 100 - Nếu ng2 SAI => phủ định của "Ít nhất hai người nói sai" => số người nói sai nhỏ hơn 2 => vô lý (vì có 2 người nói sai là ng100 và ng2) => ng2 nói đúng - Nếu ng99 Đúng => Ít nhất 99ng phát biểu sai => vô lý, vì đã có 2ng nói đúng là ng1 và ng2 nên chỉ có tối đa 98ng phát biểu sai => ng99 nói SAI - Tương tự như vậy lần lượt xét ng3 -> ng98 -> ng4 -> ng97 -> ng5 -> ng96... Ta sẽ thấy lần lượt họ nói Đúng - Sai - Đúng - Sai - Đúng - Sai... Vậy 50 người từ ng1 đến ng50 nói đúng, 50ng còn lại nói sai
Nếu người thứ n đúng, sẽ kéo theo người từ 1 đến n-1 đúng, tức là n người phát biểu đúng. Thật vậy, người thứ 40 phát biểu "có ít nhất 40 người phát biểu sai". Nếu điều đó là đúng, thì các phát biểu "có ít nhất 39. 38,... Hay có ít nhất 1 người phát biểu sai" cũng trở thành phát biểu đúng. Và trong câu nói của người thứ n, cũng khẳng định n người phát biểu sai. Vậy n phải là số thoả mãn 2*n <= 100. Suy ra, max (n) = 50. 50 người phát biểu đúng. 50 người phát biểu sai.

Tất nhiên người 1 nói đúng do đó số người nói sai (đặt là N) sẽ lớn hơn hay bằng 1. Vì chỉ có N người nói sai do đó người thứ N+1, N+2,... , 100 đã sai khi nói có ít nhất N, N+1,... , 100 người nói sai tuơng tự người thứ 1, 2,... , N đã nói đúng. Vậy số người nói sai là 100- (N+1)+1 = N. Vậy N = 50. Kết luận có 50 nguời nói đúng và 50 người nói sai.

co 25*30=750 ghe => co 680 cho ngoi kin và 70 cho ko co
ta co 680/30=22 du 20 vay co 22 hang ghe co nguoi ngoi kin bang nhau va 2 hang ghe 0 co nguoi cung co so nguoi bang nhau

nếu ta thêm 150 vào số đã cho thì ta lần lượt có:
A+150=7.a+4+150=7.a+7.22=7.(a+22)
=17.b+3+150=17.b+17.9=17.(b+9)
=23.c+11+150=23.c+23.7=23.(c+7)
như vậy A+150 đồng thời chia hết cho 7,17 và 23. nhưng 7, 17 và 23 là ba sô đôi một nguyên tố cùng nhau, suy ra A+150 chia hết cho 7.17.13=2737
vậy A+150=2737k (k=1;2;3;4...)
suy ra: A=2737k-150=2737k-2737+2587=2737(k-1)+2587=2737k'+2587
do 2587<2737 nên 2587 là số dư trong phép chia số đã cho A cho 2737

Đáp án A
Giả sử 100 đồ vật được xếp thành hàng ngang, giữa chúng có 99 khoảng trống. Đặt một cách bất kì 3 vạch vào 99 khoảng trống đó, ta được một cách chia 100 đồ vật ra thành 4 phần để lần lượt gán cho 4 người. Khi đó mỗi người được ít nhất 1 đồ vật và tổng đồ vật của 2 người bằng 100, thỏa mãn yêu cầu bài toán.
Vậy số cách chia đồ vật thỏa mãn là