Câu 1: Cho hàm số:  , TXĐ của hàm số là:
, TXĐ của hàm số là:
A.  B.
B. C.
C. D. R
D. R
Câu 2: Cho hàm số:  , TXĐ của hàm số là:
, TXĐ của hàm số là:
 A.
A.  B.
B.  C.
C.  D.
D. 
Câu 3: Cho hàm số:  , TXĐ của hàm số là:
, TXĐ của hàm số là:
A.  B.
B. C.
C.  D. R
D. R
Câu 4: Cho hàm số:  , TXĐ của hàm số là:
, TXĐ của hàm số là:
A.  B.
B.  C. D=R D.
C. D=R D. 
Câu 5: Cho hàm số:  , GTNN của hàm số là:
, GTNN của hàm số là:
A. 1 B. 2 C. 3 D. 5
Câu 6: Cho hàm số:  , GTLN của hàm số là:
, GTLN của hàm số là:
A. 2 B. 4 C. 6 D. 8
Câu 7. Giá trị lớn nhất (M), giá trị nhỏ nhất (m) của hàm số  là :
là :
A. M = 5; m = 1 B. M = 5; m = 3 C. M = 3; m = 1 D. M = 3; m = 0
Câu 8. Giá trị lớn nhất (M), giá trị nhỏ nhất (m) của hàm số  là :
là :
A. M = 1; m = -1 B. M = 2; m = 0 C. M = 2; m = 1 D. M = 1; m = 0
Câu 9. Giá trị lớn nhất (M), giá trị nhỏ nhất (m) của hàm số  là :
là :
A. M =  ; m = -1 B. M = 1; m =
; m = -1 B. M = 1; m =  C. M =
C. M =  ; m =
; m =  D. M = 1; m = -1
D. M = 1; m = -1
Câu 10. Giá trị lớn nhất (M), giá trị nhỏ nhất (m) của hàm số  trên đoạn
trên đoạn  là :
là :
A. M = 1; m = 0 B. M = 1; m = -1 C. M = 0; m = -1 D. Cả A, B, C đều sai.
Câu 11. Giá trị lớn nhất (M), giá trị nhỏ nhất (m) của hàm số  là :
là :
A. M = 8; m = 2 B. M = 5; m = 2 C. M = 8; m = 4 D. M = 8; m = 5.
Câu 12. Giá trị lớn nhất (M), giá trị nhỏ nhất (m) của hàm số  là :
là :
A. M = 3; m =  B. M =
B. M =  ; m = 1 C. M =
; m = 1 C. M =  ; m = 3 D. M = 3; m = 1.
; m = 3 D. M = 3; m = 1.
Câu 13. Giá trị lớn nhất (M), giá trị nhỏ nhất (m) của hàm số  là :
là :
A. M = 2; m =  B. M = 2; m = -2 C. M = -2; m =
B. M = 2; m = -2 C. M = -2; m =  D. M = 0; m = -2.
D. M = 0; m = -2.
Câu 14. Giá trị lớn nhất (M), giá trị nhỏ nhất (m) của hàm số  là :
là :
A. M = 0; m =  B. M = 0; m =
B. M = 0; m =  C. M =
C. M =  ; m = 0 D. M =
; m = 0 D. M =  ; m =
; m =  .
.
Câu 15.Xét hàm số  trên đoạn
trên đoạn  khẳng định nào sau đúng ?
khẳng định nào sau đúng ?
A. Trên các khoảng  hàm số luôn đồng biến.
hàm số luôn đồng biến.
B. Trên khoảng  hàm số đồng biến và trên khoảng
hàm số đồng biến và trên khoảng  hàm số nghịch biến.
hàm số nghịch biến.
C. Trên khoảng  hàm số nghịch biến và trên khoảng
hàm số nghịch biến và trên khoảng  hàm số đồng biến.
hàm số đồng biến.
D. Trên các khoảng  hàm số luôn nghịch biến.
hàm số luôn nghịch biến.
Câu 16.Xét hàm số  trên đoạn
trên đoạn  khẳng định nào sau đúng ?
khẳng định nào sau đúng ?
A. Trên các khoảng  hàm số luôn nghịch biến.
hàm số luôn nghịch biến.
B. Trên khoảng  hàm số đồng biến và trên khoảng
hàm số đồng biến và trên khoảng  hàm số nghịch biến.
hàm số nghịch biến.
C. Trên khoảng  hàm số nghịch biến và trên khoảng
hàm số nghịch biến và trên khoảng  hàm số đồng biến.
hàm số đồng biến.
D. Trên các khoảng  hàm số luôn đồng biến.
hàm số luôn đồng biến.
Câu 17.Xét hàm số  trên khoảng
trên khoảng  khẳng định nào sau đúng ?
khẳng định nào sau đúng ?
A. Trên khoảng  hàm số luôn đồng biến.
hàm số luôn đồng biến.
B. Trên khoảng  hàm số đồng biến và trên khoảng
hàm số đồng biến và trên khoảng  hàm số nghịch biến.
hàm số nghịch biến.
C. Trên khoảng  hàm số nghịch biến và trên khoảng
hàm số nghịch biến và trên khoảng  hàm số đồng biến.
hàm số đồng biến.
D. Trên các khoảng  hàm số luôn nghịch biến.
hàm số luôn nghịch biến.
Câu 18.Xét hàm số  trên khoảng
trên khoảng  khẳng định nào sau đúng ?
khẳng định nào sau đúng ?
A. Trên khoảng  hàm số luôn đồng biến.
hàm số luôn đồng biến.
B. Trên khoảng  hàm số đồng biến và trên khoảng
hàm số đồng biến và trên khoảng  hàm số nghịch biến.
hàm số nghịch biến.
C. Trên khoảng  hàm số nghịch biến và trên khoảng
hàm số nghịch biến và trên khoảng  hàm số đồng biến.
hàm số đồng biến.
D. Trên các khoảng  hàm số luôn nghịch biến.
hàm số luôn nghịch biến.
Câu 19. Chọn khẳng định sai về tính chẵn lẻ của các hàm số trong các khẳng định sau :
A. Hàm số  là hàm số lẻ. B. Hàm số
là hàm số lẻ. B. Hàm số  là hàm số chẵn.
là hàm số chẵn.
C. Hàm số  là hàm số chẵn. D. Hàm số
là hàm số chẵn. D. Hàm số  là hàm số lẻ .
là hàm số lẻ .
Câu 1: Cho hàm số:  , TXĐ của hàm số là:
, TXĐ của hàm số là:
A.  B.
B. C.
C. D. R
D. R
Câu 2: Cho hàm số:  , TXĐ của hàm số là:
, TXĐ của hàm số là:
 A.
A.  B.
B.  C.
C.  D.
D. 
Câu 3: Cho hàm số:  , TXĐ của hàm số là:
, TXĐ của hàm số là:
A.  B.
B. C.
C.  D. R
D. R
Câu 4: Cho hàm số:  , TXĐ của hàm số là:
, TXĐ của hàm số là:
A.  B.
B.  C. D=R D.
C. D=R D. 
Câu 5: Cho hàm số:  , GTNN của hàm số là:
, GTNN của hàm số là:
A. 1 B. 2 C. 3 D. 5
Câu 6: Cho hàm số:  , GTLN của hàm số là:
, GTLN của hàm số là:
A. 2 B. 4 C. 6 D. 8
Câu 7. Giá trị lớn nhất (M), giá trị nhỏ nhất (m) của hàm số  là :
là :
A. M = 5; m = 1 B. M = 5; m = 3 C. M = 3; m = 1 D. M = 3; m = 0
Câu 8. Giá trị lớn nhất (M), giá trị nhỏ nhất (m) của hàm số  là :
là :
A. M = 1; m = -1 B. M = 2; m = 0 C. M = 2; m = 1 D. M = 1; m = 0
Câu 9. Giá trị lớn nhất (M), giá trị nhỏ nhất (m) của hàm số  là :
là :
A. M =  ; m = -1 B. M = 1; m =
; m = -1 B. M = 1; m =  C. M =
C. M =  ; m =
; m =  D. M = 1; m = -1
D. M = 1; m = -1
Câu 10. Giá trị lớn nhất (M), giá trị nhỏ nhất (m) của hàm số  trên đoạn
trên đoạn  là :
là :
A. M = 1; m = 0 B. M = 1; m = -1 C. M = 0; m = -1 D. Cả A, B, C đều sai.
Câu 11. Giá trị lớn nhất (M), giá trị nhỏ nhất (m) của hàm số  là :
là :
A. M = 8; m = 2 B. M = 5; m = 2 C. M = 8; m = 4 D. M = 8; m = 5.
Câu 12. Giá trị lớn nhất (M), giá trị nhỏ nhất (m) của hàm số  là :
là :
A. M = 3; m =  B. M =
B. M =  ; m = 1 C. M =
; m = 1 C. M =  ; m = 3 D. M = 3; m = 1.
; m = 3 D. M = 3; m = 1.
Câu 13. Giá trị lớn nhất (M), giá trị nhỏ nhất (m) của hàm số  là :
là :
A. M = 2; m =  B. M = 2; m = -2 C. M = -2; m =
B. M = 2; m = -2 C. M = -2; m =  D. M = 0; m = -2.
D. M = 0; m = -2.
Câu 14. Giá trị lớn nhất (M), giá trị nhỏ nhất (m) của hàm số  là :
là :
A. M = 0; m =  B. M = 0; m =
B. M = 0; m =  C. M =
C. M =  ; m = 0 D. M =
; m = 0 D. M =  ; m =
; m =  .
.
Câu 15.Xét hàm số  trên đoạn
trên đoạn  khẳng định nào sau đúng ?
khẳng định nào sau đúng ?
A. Trên các khoảng  hàm số luôn đồng biến.
hàm số luôn đồng biến.
B. Trên khoảng  hàm số đồng biến và trên khoảng
hàm số đồng biến và trên khoảng  hàm số nghịch biến.
hàm số nghịch biến.
C. Trên khoảng  hàm số nghịch biến và trên khoảng
hàm số nghịch biến và trên khoảng  hàm số đồng biến.
hàm số đồng biến.
D. Trên các khoảng  hàm số luôn nghịch biến.
hàm số luôn nghịch biến.
Câu 16.Xét hàm số  trên đoạn
trên đoạn  khẳng định nào sau đúng ?
khẳng định nào sau đúng ?
A. Trên các khoảng  hàm số luôn nghịch biến.
hàm số luôn nghịch biến.
B. Trên khoảng  hàm số đồng biến và trên khoảng
hàm số đồng biến và trên khoảng  hàm số nghịch biến.
hàm số nghịch biến.
C. Trên khoảng  hàm số nghịch biến và trên khoảng
hàm số nghịch biến và trên khoảng  hàm số đồng biến.
hàm số đồng biến.
D. Trên các khoảng  hàm số luôn đồng biến.
hàm số luôn đồng biến.
Câu 17.Xét hàm số  trên khoảng
trên khoảng  khẳng định nào sau đúng ?
khẳng định nào sau đúng ?
A. Trên khoảng  hàm số luôn đồng biến.
hàm số luôn đồng biến.
B. Trên khoảng  hàm số đồng biến và trên khoảng
hàm số đồng biến và trên khoảng  hàm số nghịch biến.
hàm số nghịch biến.
C. Trên khoảng  hàm số nghịch biến và trên khoảng
hàm số nghịch biến và trên khoảng  hàm số đồng biến.
hàm số đồng biến.
D. Trên các khoảng  hàm số luôn nghịch biến.
hàm số luôn nghịch biến.
Câu 18.Xét hàm số  trên khoảng
trên khoảng  khẳng định nào sau đúng ?
khẳng định nào sau đúng ?
A. Trên khoảng  hàm số luôn đồng biến.
hàm số luôn đồng biến.
B. Trên khoảng  hàm số đồng biến và trên khoảng
hàm số đồng biến và trên khoảng  hàm số nghịch biến.
hàm số nghịch biến.
C. Trên khoảng  hàm số nghịch biến và trên khoảng
hàm số nghịch biến và trên khoảng  hàm số đồng biến.
hàm số đồng biến.
D. Trên các khoảng  hàm số luôn nghịch biến.
hàm số luôn nghịch biến.
Câu 19. Chọn khẳng định sai về tính chẵn lẻ của các hàm số trong các khẳng định sau :
A. Hàm số  là hàm số lẻ. B. Hàm số
là hàm số lẻ. B. Hàm số  là hàm số chẵn.
là hàm số chẵn.
C. Hàm số  là hàm số chẵn. D. Hàm số
là hàm số chẵn. D. Hàm số  là hàm số lẻ .
là hàm số lẻ .
Câu 1: Cho hàm số:  , TXĐ của hàm số là:
, TXĐ của hàm số là:
A.  B.
B. C.
C. D. R
D. R
Câu 2: Cho hàm số:  , TXĐ của hàm số là:
, TXĐ của hàm số là:
 A.
A.  B.
B.  C.
C.  D.
D. 
Câu 3: Cho hàm số:  , TXĐ của hàm số là:
, TXĐ của hàm số là:
A.  B.
B. C.
C.  D. R
D. R
Câu 4: Cho hàm số:  , TXĐ của hàm số là:
, TXĐ của hàm số là:
A.  B.
B.  C. D=R D.
C. D=R D. 
Câu 5: Cho hàm số:  , GTNN của hàm số là:
, GTNN của hàm số là:
A. 1 B. 2 C. 3 D. 5
Câu 6: Cho hàm số:  , GTLN của hàm số là:
, GTLN của hàm số là:
A. 2 B. 4 C. 6 D. 8
Câu 7. Giá trị lớn nhất (M), giá trị nhỏ nhất (m) của hàm số  là :
là :
A. M = 5; m = 1 B. M = 5; m = 3 C. M = 3; m = 1 D. M = 3; m = 0
Câu 8. Giá trị lớn nhất (M), giá trị nhỏ nhất (m) của hàm số  là :
là :
A. M = 1; m = -1 B. M = 2; m = 0 C. M = 2; m = 1 D. M = 1; m = 0
Câu 9. Giá trị lớn nhất (M), giá trị nhỏ nhất (m) của hàm số  là :
là :
A. M =  ; m = -1 B. M = 1; m =
; m = -1 B. M = 1; m =  C. M =
C. M =  ; m =
; m =  D. M = 1; m = -1
D. M = 1; m = -1
Câu 10. Giá trị lớn nhất (M), giá trị nhỏ nhất (m) của hàm số  trên đoạn
trên đoạn  là :
là :
A. M = 1; m = 0 B. M = 1; m = -1 C. M = 0; m = -1 D. Cả A, B, C đều sai.
Câu 11. Giá trị lớn nhất (M), giá trị nhỏ nhất (m) của hàm số  là :
là :
A. M = 8; m = 2 B. M = 5; m = 2 C. M = 8; m = 4 D. M = 8; m = 5.
Câu 12. Giá trị lớn nhất (M), giá trị nhỏ nhất (m) của hàm số  là :
là :
A. M = 3; m =  B. M =
B. M =  ; m = 1 C. M =
; m = 1 C. M =  ; m = 3 D. M = 3; m = 1.
; m = 3 D. M = 3; m = 1.
Câu 13. Giá trị lớn nhất (M), giá trị nhỏ nhất (m) của hàm số  là :
là :
A. M = 2; m =  B. M = 2; m = -2 C. M = -2; m =
B. M = 2; m = -2 C. M = -2; m =  D. M = 0; m = -2.
D. M = 0; m = -2.
Câu 14. Giá trị lớn nhất (M), giá trị nhỏ nhất (m) của hàm số  là :
là :
A. M = 0; m =  B. M = 0; m =
B. M = 0; m =  C. M =
C. M =  ; m = 0 D. M =
; m = 0 D. M =  ; m =
; m =  .
.
Câu 15.Xét hàm số  trên đoạn
trên đoạn  khẳng định nào sau đúng ?
khẳng định nào sau đúng ?
A. Trên các khoảng  hàm số luôn đồng biến.
hàm số luôn đồng biến.
B. Trên khoảng  hàm số đồng biến và trên khoảng
hàm số đồng biến và trên khoảng  hàm số nghịch biến.
hàm số nghịch biến.
C. Trên khoảng  hàm số nghịch biến và trên khoảng
hàm số nghịch biến và trên khoảng  hàm số đồng biến.
hàm số đồng biến.
D. Trên các khoảng  hàm số luôn nghịch biến.
hàm số luôn nghịch biến.
Câu 16.Xét hàm số  trên đoạn
trên đoạn  khẳng định nào sau đúng ?
khẳng định nào sau đúng ?
A. Trên các khoảng  hàm số luôn nghịch biến.
hàm số luôn nghịch biến.
B. Trên khoảng  hàm số đồng biến và trên khoảng
hàm số đồng biến và trên khoảng  hàm số nghịch biến.
hàm số nghịch biến.
C. Trên khoảng  hàm số nghịch biến và trên khoảng
hàm số nghịch biến và trên khoảng  hàm số đồng biến.
hàm số đồng biến.
D. Trên các khoảng  hàm số luôn đồng biến.
hàm số luôn đồng biến.
Câu 17.Xét hàm số  trên khoảng
trên khoảng  khẳng định nào sau đúng ?
khẳng định nào sau đúng ?
A. Trên khoảng  hàm số luôn đồng biến.
hàm số luôn đồng biến.
B. Trên khoảng  hàm số đồng biến và trên khoảng
hàm số đồng biến và trên khoảng  hàm số nghịch biến.
hàm số nghịch biến.
C. Trên khoảng  hàm số nghịch biến và trên khoảng
hàm số nghịch biến và trên khoảng  hàm số đồng biến.
hàm số đồng biến.
D. Trên các khoảng  hàm số luôn nghịch biến.
hàm số luôn nghịch biến.
Câu 18.Xét hàm số  trên khoảng
trên khoảng  khẳng định nào sau đúng ?
khẳng định nào sau đúng ?
A. Trên khoảng  hàm số luôn đồng biến.
hàm số luôn đồng biến.
B. Trên khoảng  hàm số đồng biến và trên khoảng
hàm số đồng biến và trên khoảng  hàm số nghịch biến.
hàm số nghịch biến.
C. Trên khoảng  hàm số nghịch biến và trên khoảng
hàm số nghịch biến và trên khoảng  hàm số đồng biến.
hàm số đồng biến.
D. Trên các khoảng  hàm số luôn nghịch biến.
hàm số luôn nghịch biến.
Câu 19. Chọn khẳng định sai về tính chẵn lẻ của các hàm số trong các khẳng định sau :
A. Hàm số  là hàm số lẻ. B. Hàm số
là hàm số lẻ. B. Hàm số  là hàm số chẵn.
là hàm số chẵn.
C. Hàm số  là hàm số chẵn. D. Hàm số
là hàm số chẵn. D. Hàm số  là hàm số lẻ .
là hàm số lẻ .









 . Tính
. Tính 

 .
. . Tính
. Tính  bằng:
bằng:
 bằng:
bằng:

 .
.
Đáp án D
Số phần tử của không gian mẫu là .
.
Bộ 3 số có tổng chia hết cho 3 sẽ có bộ số dư là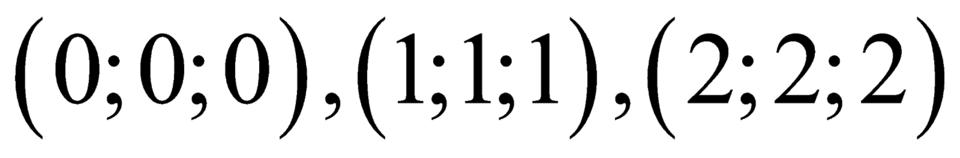 và
và 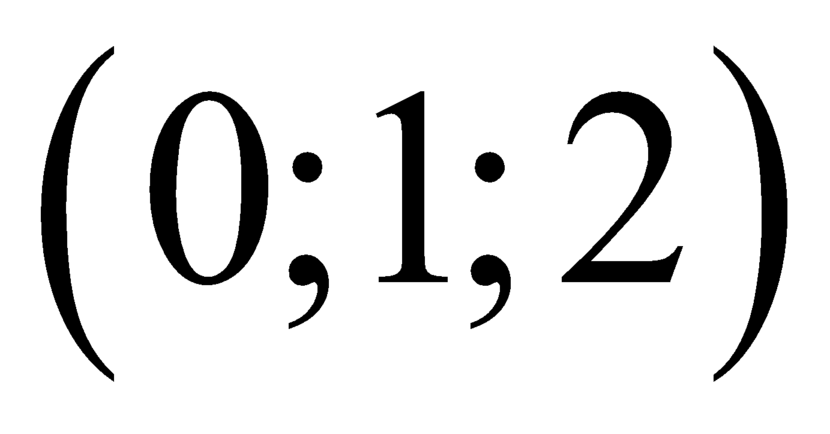 .
.
Trong các số từ 1 đến 60 có 20 số chia hết cho 3, 20 số chia 3 dư 1 và 20 số chia 3 dư 2.
Vậy số cách chọ ra bộ 3 tấm thẻ có tổng các số trên thẻ chia hết cho 3 là
Vậy xác suất cần tính là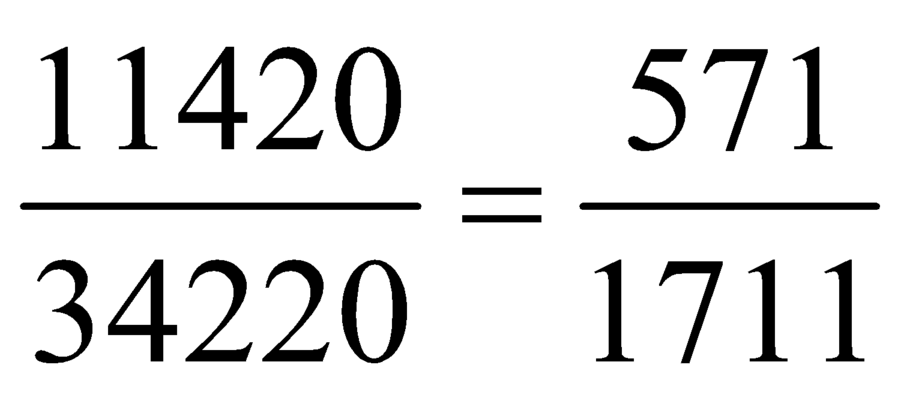 .
.