Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số cách chia là:
\(A^7_{10}=604800\left(cách\right)\)

Đáp án B
30 quyển sách chia thành 15 bộ gồm :
+) 6 bộ giống nhau gồm 1 Toán- 1 Lý
+) 5 bộ giống nhau gồm 1 Lý – 1 Hóa
+) 4 bộ giống nhau gồm 1 Toán – 1 Hóa
Chọn 6 học sinh trong 15 học sinh để trao bộ Toán- Lý có C 15 6 cách
Chọn 5 học sinh trong 9 học sinh còn lại để trao bộ Lý- Hóa có C 9 5 cách
Vậy 4 học sinh còn lại sẽ được nhận bộ Toán – Hóa. Vậy có C 15 6 . C 9 5 cách trao thưởng.

Bước 1: Do đề bài cho 4 quyển sách Toán đứng cạnh nhau nên ta sẽ coi như “buộc” các quyển sách Toán lại với nhau thì số cách xếp cho “buộc” Toán này là 4! cách.
Bước 2: Tương tự ta cũng “buộc” 3 quyển sách Lý lại với nhau, thì số cách xếp cho “buộc” Lý này là 3! cách.
Bước 3: Lúc này ta sẽ đi xếp vị trí cho 7 phần tử trong đó có:
+ 1 “buộc” Toán.
+ 1 “buộc” Lý.
+ 5 quyển Hóa.
Thì sẽ có 7! cách xếp.
Vậy theo quy tắc nhân ta có 7!4!3!=725760 cách xếp.
Chọn C.

Chọn B
Không gian mẫu là tập hợp tất cả các cách xếp 4 quyển Toán khác nhau và 4 quyển Hóa giống nhau vào 8 trong 10 ô trống.
Khi đó, ![]()
Gọi A là biến cố: “ Bốn quyển sách Toán xếp cạnh nhau và 4 quyển sách Hóa xếp cạnh nhau ”.
Để xếp 4 quyển sách Toán cạnh nhau và 4 quyển sách Hóa gần nhau trên giá sách 10 ô trống ta xem như có 4 vị trí để xếp
Xếp 4 quyển toán cạnh nhau có 4! cách, xếp 4 quyển Hóa có 1 cách, sau đó xếp 2 bộ đó vào 2 trong 4 vị trí.
Do đó: ![]()
Xác suất để 4 quyển sách Toán cạnh nhau và 4 quyển Hóa cạnh nhau là:


Lời giải:
Chọn 4 quyển sách khác nhau đủ 3 loại, có các TH sau:
TH1: 1 toán, 1 lý, 2 hóa: $A_1=C^1_6.C^1_7.C^2_8$ cách
TH2: 2 toán, 1 lý, 1 hóa: $A_2=C^2_6.C^1_7.C^1_8$ cách
TH3: 1 toán, 2 lý, 1 hóa: $A_3=C^1_6.C^2_7.C^1_8$ cách
Tổng số cách: $A_1+A_2+A_3=3024$ cách

Chọn A.
Lời giải.
Không gian mẫu là số cách chọn 2 phần thưởng trong số 12 phần thưởng
Suy ra số phần tử của không gian mẫu là Ω = C 12 2 = 66
Gọi A là biến cố ""Bạn An và bạn Bình có phần thưởng giống nhau"".
Để tìm số phần tử của A, ta làm như sau
Gọi x là cặp số gồm 2 quyển Toán và Vật Lí
y là số cặp gồm 2 quyển Toán và Hóa Học;
z là số cặp gồm 2 quyển Vật Lí và Hóa Học
Ta có hệ phương trình
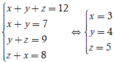
Suy ra số phần tử của biến cố A là
Ω A = C 3 2 + C 4 2 + C 5 2
Vậy xác suất cần tính P ( A ) = 19 66
