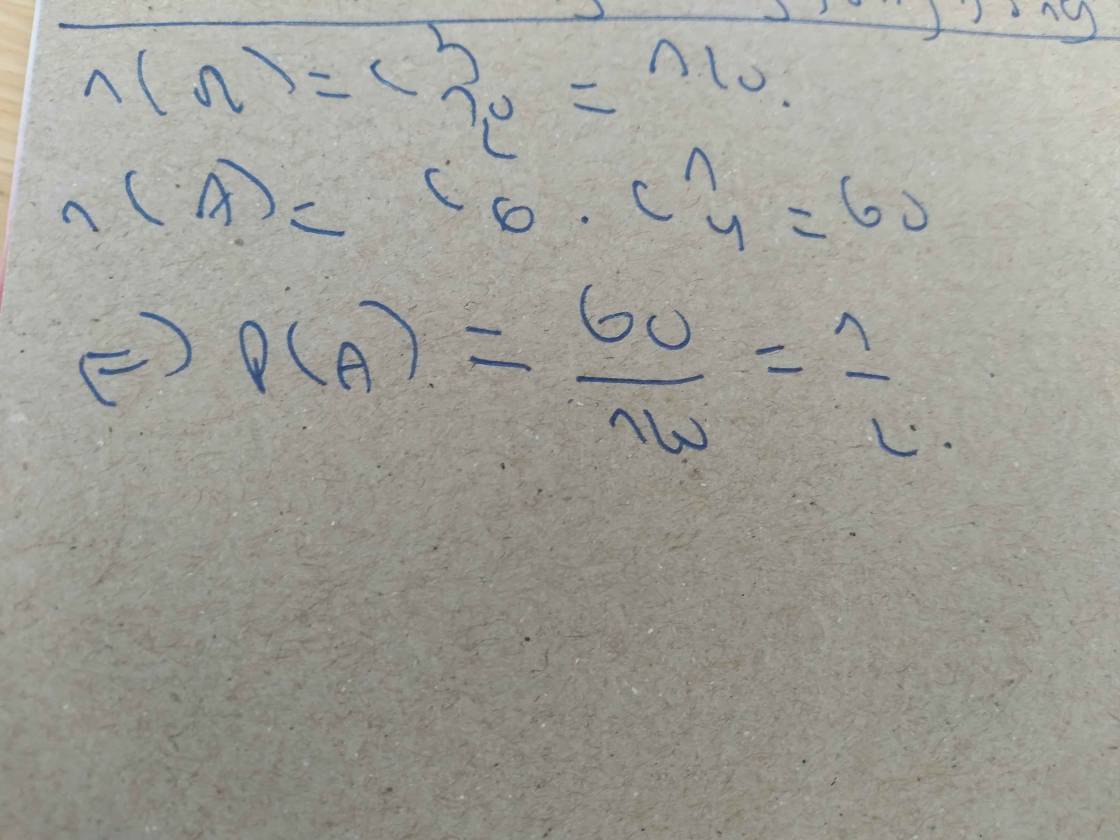Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Số cách chọn là: \(C^3_{25}=2300\left(cách\right)\)
b: Số cách chọn là: \(C^1_{15}\cdot C^2_{24}=4140\left(cách\right)\)

a: SỐ cách xếp là;
5!*6!*2=172800(cách)
b: Số cách xếp là \(6!\cdot5!=86400\left(cách\right)\)

Xếp 4 bạn nữ: có \(4!\) cách
4 bạn nữ tạo ra 5 khe trống, xếp 2 bạn nam vào 5 khe trống đó: \(A_5^2\) cách
Vậy tổng cộng có \(4!.A_5^2\) cách xếp thỏa mãn

Chọn A có 1 cách, chọn B có 1 cách
Chọn 2 bạn bất kì từ 6 bạn còn lại (4 nữ và 2 nam): \(C_6^2\) cách
Vậy có \(1.1.C_6^2=15\) cách

\(\Omega \) là tập tất cả 6 học sinh trong 12 học sinh. Vậy \(n\left( \Omega \right) = C_{12}^6 = 924\).
Gọi C là biến cố: “Có 3 học sinh nam và 3 học sinh nữ”. Có \(C_7^3\) cách chọn chọn 3 học sinh nam và \(C_5^3\) cách chọn 3 học sinh nữ. Theo quy tắc nhân, ta có \(C_7^3.C_5^3 = 350\) cách chọn 3 học sinh nam và 3 học sinh nữ tức là \(n\left( C \right) = 350\).Vậy \(P\left( C \right) = \frac{{350}}{{924}} \approx 0,3788\).

Số cách chọn là:
\(C^1_4\cdot C^2_5+C^2_4\cdot5+C^3_4=74\left(cách\right)\)

1. Đã giải
2.
Xếp 10 cái bánh thành hàng ngang, 10 cái bánh tạo ra 9 khe trống (mà khe trống này nằm giữa 2 cái bánh)
Đặt 2 vách ngăn vào 9 vị trí nói trên, 2 vách ngăn sẽ chia 10 cái bánh làm 3 phần sao cho mỗi phần có ít nhất 1 cái bánh. Vậy có \(C_9^2\) cách đặt 2 vách ngăn hay có \(C_9^2\) cách chia 10 cái bánh cho 3 người sao cho mỗi người có ít nhất 1 cái bánh.

Không gian mẫu: \(C_{10}^3\)
Số cách chọn sao cho có 2 nữ 1 nam là: \(C_6^2.C_4^1\)
Xác suất: \(P=\dfrac{C_6^2.C_4^1}{C_{10}^3}=\dfrac{1}{2}\)

Chọn hai học sinh từ tổ sao cho 2 học sinh cùng giới có 2 công đoạn
\(CD_1:\) Chọn 1 bạn nữ trong 5 bạn nữ \(\Rightarrow\) Có 5 cách chọn
\(CD_2:\) Chọn 1 bạn nam trong 4 bạn nam \(\Rightarrow\) Có 4 cách chọn
Áp dụng quy tắc nhân, ta có : \(5.4=20\) ( cách chọn )
Vậy có 20 cách chọn 2 học sinh từ tổ để 1 bàn có 2 học sinh cùng giới
Lời giải:
Chọn 2 học sinh cùng giới tính nam, có: $C^2_4=6$ cách
Chọn 2 học sinh cùng giới tính nữ, có: $C^2_5=10$ cách
Tổng số cách chọn: $6+10=16$ (cách)