Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+) Số cách chọn 3hs bất kì trong 34hs là: \(C_{34}^3\) ( cách chọn)
+) Số cách chọn 3hs nam trong 34hs là: \(C_{18}^3\) ( cách chọn)
+) Số cách chọn 3hs nữ trong 34hs là: \(C_{16}^3\) ( cách chọn)
+) Số cách chọn 3hs gồm cả nam và nữ trong 34hs là: \(C_{34}^3 - C_{18}^3 - C_{16}^3 = 4608\) ( cách chọn)

Gọi số học sinh của 3 lớp lần lượt là a, b và c.
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{a}{9}=\frac{b}{10}=\frac{c}{11}=\frac{a+b+c}{9+10+11}=\frac{120}{30}=4\)
\(\frac{a}{9}=4\Rightarrow a=36\)
\(\frac{b}{10}=4\Rightarrow b=40\)
\(\frac{c}{11}=4\Rightarrow c=44\)
Vậy số học sinh của 3 lớp lần lượt là 36 , 40 và 44.
Gọi số học sinh 3 lớp 7A;7B;7C lần lượt là a;b;c
Theo đề ra ta có
\(\frac{a}{9}=\frac{b}{10}=\frac{c}{11}\)
\(\Rightarrow\frac{a}{9}=\frac{b}{10}=\frac{c}{11}=\frac{a+b+c}{9+10+11}=\frac{120}{30}=4\)
\(\Rightarrow\begin{cases}a=36\\b=40\\c=44\end{cases}\)
Vậy lớp 7A : 36 hs
7B:40 hs
7C:44 hs

Đáp án A
Theo giả thiết đề bài cho, ta có biểu đồ Ven:
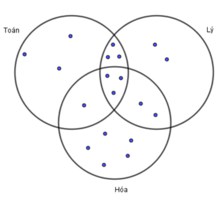
Dựa vào biểu đồ Ven ta thấy:
Số học sinh chỉ giỏi Toán và Lý (không giỏi Hóa) là: 6−3=3 (em)
Số học sinh chỉ giỏi Toán và Hóa (không giỏi Lý) là: 4−3=1 (em)
Số học sinh chỉ giỏi Lý và Hóa (không giỏi Toán) là: 5−3=2 (em)
Số học sinh chỉ giỏi một môn Toán là: 10−3−3−1=3 (em)
Số học sinh chỉ giỏi một môn Lý là: 10−3−3−2=2 (em)
Số học sinh chỉ giỏi một môn Hóa là: 11−1−3−2=5 (em)
Số học sinh giỏi ít nhất một trong ba môn là:
3+2+5+1+2+3+3=19 (em)

Goi số học sinh 3 lớp lần lượt là a;b;c
(+)
\(2a+3b-4c=19\)
(+)
\(\Rightarrow a=\frac{14}{15}b\)
\(\Rightarrow\frac{a}{14}=\frac{b}{15}\)
\(\Rightarrow\frac{a}{84}=\frac{b}{90}\)(1)
(+)
\(\Rightarrow b=\frac{9}{10}c\)
\(\Rightarrow\frac{b}{9}=\frac{c}{10}\)
\(\Rightarrow\frac{b}{90}=\frac{a}{100}\)(1)
Từ (1) và (2)
=>\(\frac{a}{84}=\frac{b}{90}=\frac{c}{100}\)
=>\(\frac{2a}{168}=\frac{3b}{180}=\frac{4c}{400}\)
Áp dụng tc của dãy tỉ số bằng nhau ta có
\(\frac{2a}{168}=\frac{3b}{270}=\frac{4c}{400}=\frac{2a+3b-4c}{168+270-400}=\frac{19}{38}=\frac{1}{2}\)
\(\Rightarrow\begin{cases}a=42\\b=45\\c=50\end{cases}\)
Vậy số học sinh 3 lớp lần lượt là 42;45;50


