Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số kết quả có thể là C520C205.
Số kết quả thuận lợi là số cách chọn 5 số trong tập [1,2,…,10][1,2,…,10]. Do đó, số kết quả thuận lợi là C510C105.
Vậy xác suất cần tìm là C510C520≈0,016
đúng ko

Không gian mẫu là kết quả của việc sắp xếp 10 người theo 1 thứ tự.
⇒ n(Ω) = P10 = 10! = 3 628 800.
a) Gọi M: “A và B đứng liền nhau”
* Coi A và B là một phần tử X.
Số cách xếp X và 8 người khác thành hàng dọc là: 9!
Số cách xếp hai người A và B là: 2!= 2 cách
Theo quy tắc nhân có: 9!.2= 725760 cách xếp thỏa mãn
Xác suất của biến cố M là: 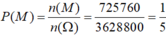
b) Gọi N: “Trong hai người đó có một người đứng ở vị trí số 1 và một người kia đứng ở vị trí cuối cùng”.
+ Sắp xếp vị trí cho A và B: Có 2 cách
+ Sắp xếp vị trí cho 8 người còn lại: có 8! cách
⇒ Theo quy tắc nhân: n(N) = 2.8!
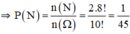

2, sin4x+cos5=0 <=> cos5x=cos\(\left(\frac{\pi}{2}+4x\right)\Leftrightarrow\orbr{\begin{cases}x=\frac{\pi}{2}+k2\pi\\x=-\frac{\pi}{18}+\frac{k2\pi}{9}\end{cases}\left(k\inℤ\right)}\)
ta có \(2\pi>0\Leftrightarrow k< >\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(\frac{\pi}{2}\)khi k=0
\(-\frac{\pi}{18}+\frac{k2\pi}{9}>0\Leftrightarrow k>\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(-\frac{\pi}{18}-\frac{k2\pi}{9}\)là \(\frac{\pi}{6}\)khi k=1
vậy nghiệm dương nhỏ nhất của phương trình là \(\frac{\pi}{6}\)
\(\frac{\pi}{2}+k2\pi< 0\Leftrightarrow k< -\frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(\frac{\pi}{2}+k2\pi\)là \(-\frac{3\pi}{2}\)khi k=-1
\(-\frac{\pi}{18}+\frac{k2\pi}{9}< 0\Leftrightarrow k< \frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(-\frac{\pi}{18}+\frac{k2\pi}{9}\)là \(-\frac{\pi}{18}\)khi k=0
vậy nghiệm âm lớn nhất của phương trình là \(-\frac{\pi}{18}\)

Câu 1:
Khong gian mẫu: \(C_{11}^3\)
Có 5 cặp bi cùng số, do đó có \(5\) cách chọn ra 1 cặp cùng số, viên còn lại có 9 cách chọn \(\Rightarrow\) có 45 cách chọn 3 viên có 2 viên cùng số (tất nhiên là ko thể 3 viên cùng số được)
Xác suất: \(P=\frac{C_{11}^3-45}{C_{11}^3}=\frac{8}{11}\)
Câu 2:
Không gian mẫu: \(9!\)
Xếp 4 bạn nam cạnh nhau và hoán vị, có \(4!\) cách
Coi 4 bạn nam này là 1 người, xếp hàng cùng 5 bạn nữ \(\Rightarrow\) có \(6!\) cách hoán vị
Vậy có \(4!.6!\) cách
Xác suất: \(P=\frac{4!.6!}{9!}=\frac{1}{21}\)

Chọn C
Ta có: ![]()
Gọi A là biến cố “trong 3 người được chọn đó không có 2 người ngồi kề nhau”
=> A ¯ là biến cố “trong 3 người đươc chọn có ít nhất 2 người ngồi kề nhau”
![]()

TH 1: 3 người ngồi kề nhau có 13 cách chọn.
TH 2: có 2 người ngồi cạnh nhau
- Hai người ngồi cạnh nhau ngồi đầu hàng có 2 cách chọn, với mỗi cách chọn như vậy có 12 cách chọn người còn lại vậy có: 2.12=24 cách.
- Hai người ngồi cạnh nhau không ngồi đầu hàng có 12 cách chọn, với mỗi cách chọn như vậy có 11 cách chọn người còn lại vậy có: 11.12=132 cách.
![]()
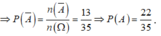
Đáp án B
Có n ( Ω ) = C 12 3
Giả sử chọn 3 người có số thứ tự trong hàng lần lượt là a, b, c
Theo giả thiết ta có: a < b < c, b – a > 1, c – b > 1, a , b , c ∈ { 1 , 2 , . . . , 12 } .