Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tập xác định: D = R ∖ { 1 }
· y ' = m x 2 + 2 m x + 1 x + 1 2
· Hàm số luôn đồng biến trên từng khoảng xác định của nó khi và chỉ khi y ' > 0; ∀ x ≠ 1
· Xét m = 0, ta có y ' = 1 x + 1 2 > 0 ; ∀ x ≠ 1 (tm).
· Xét m ≠ 0 .Yêu cầu bài toán
⇔ ∆ ' = m 2 - m ≤ 0 m > 0 ⇔ 0 ≤ m ≤ 1 m > 0 ⇔ 0 < m ≤ 1
Kết luận: 0 ≤ m ≤ 1
Đáp án B

a) ĐK: x-1 khác 0 và x+1 khác 0
<=> x khác 1 và x khác -1
b) ĐK: x-2 khác 0
<=> x khác 2

Đáp án A
T X D : D = ℝ \ 1
Ta có: y = m x 2 − m + 2 x + m 2 − 2 m + 2 x − 1 = m x − 2 + m 2 − 2 m x − 1 ⇒ y ' = m − m 2 − 2 m x − 1 2
hàm số luôn đồng biến trên tập xác định của nó khi y ' ≥ 0 ∀ x ∈ D (dấu bằng xảy ra tại hữu hạn điểm)
⇔ m − m 2 − 2 m x − 1 2 ≥ 0 ∀ x ∈ D ⇔ x x − 1 2 ≥ m 2 − 2 m ∀ x ∈ D
Với m = 0 ⇒ y ' = 0 ∀ x ∈ D (không thỏa mãn dấu bằng xảy ra tại hữu hạn điểm)
Khi đó hàm số luôn đồng biến trên tập xác định m > 0 m 2 − 2 m ≤ 0 ⇔ 0 < m ≤ 2

\(y'=3x^2-6x+m\)
để hàm số đồng biến trên R thì y'>0 với mọi x thuộc R
suy ra \(\begin{cases}3>0\\\Delta=9-3m<0\end{cases}\) suy ra m>3
vậy m>3 là điều cần tìm

Ta có y'=\(\frac{1}{2}\frac{3-2x}{\sqrt{3x-x^2}}\)
vì 3-2x<0 trên đoạn \(\left[\frac{3}{2};2\right]\) suy ra y'<0 với mọi x thuộc \(\left[\frac{3}{2};2\right]\)
suy ra hàm số nghịch biến trên đoạn \(\left[\frac{3}{2};2\right]\)
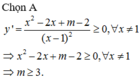
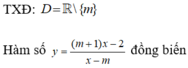
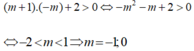
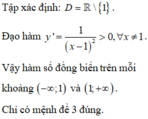
điều kiện để hàm số đơn điệu trên một khoảng là
a, nếu f'(x)>0 với mọi x thuộc khoảng đó thì hàm số đồng biến trên khoảng đó
b, nếu f'(x)<0 với mọi x thuộc khoảng đó thì hàm số nghịch biến trên khoảng đó
c, nếu f'(x)=0 với mọi x thuộc khoảng đó thì hàm số không đổi trên khoảng đó
áp dụng vào bài trên ta có
f'(x)=\(\frac{4x^2+4x+3}{\left(2x+1\right)^2}>0\) với mọi x\(\pm\)\(\frac{-1}{2}\)
vậy hàm số đồng biến trên \(R\backslash\left\{\frac{-1}{2}\right\}\)