TG
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
19 tháng 1 2017
+ Nếu \(a\)\(;\)\(b\) không chia hết cho 3 \(\Rightarrow\) \(a^2;\)\(b^2\)chia 3 dư 1
khi đó \(a^2+b^2\) chia 3 dư 2 \(\Rightarrow\)\(c^2\) chia 3 dư 2 (vô lý)
\(\Rightarrow\)trường hợp \(a\)và \(b\) không chia hết cho 3 không xảy ra \(\Rightarrow\) \(abc\)\(⋮\)\(3\) \(\left(1\right)\)
+ Nếu \(a\)\(;\)\(b\) không chia hết cho 5 \(\Rightarrow\)\(a^2\) chia 5 dư 1 hoặc 4 cà \(b^2\) chia 5 dư 1 hoặc 4
- Nếu \(a^2\) chia 5 dư 1 và \(b^2\) chia 5 dư 1 \(\Rightarrow\) \(c^2\) chia 5 dư 2 (vô lí)
- Nếu \(a^2\) chia 5 dư 1 và \(b^2\) chia 5 dư 4 \(\Rightarrow\) \(c^2\) chia 5 dư 0 \(\Rightarrow\) \(c\)\(⋮\)\(5\)
- Nếu \(a^2\) chia 5 dư 4 và \(b^2\) chia 5 dư 1 \(\Rightarrow\) \(c^2\) chia 5 dư 0 \(\Rightarrow\) \(c\) \(⋮\)\(5\)
- Nếu \(a^2\) chia 5 dư 4 và \(b^2\) chia 5 dư 4 \(\Rightarrow\) \(c^2\) chia 5 dư 3 (vô lí). Vậy ta luôn tìm được một giá trị của \(a,\)\(b,\)\(c\)thỏa mãn \(abc\)\(⋮\)\(5\) \(\left(2\right)\)
+ Nếu \(a,\)\(b,\)\(c\) không chia hết cho 4 \(\Rightarrow\) \(a^2,\)\(b^2,\)\(c^2\) chia 8 dư 1 hoặc 4
khi đó \(a^2+b^2\) chia 8 dư \(0,\)\(2\)hoặc
\(\Rightarrow\) c2:5 dư 1,4. vô lý => a hoặc b hoặc c chia hết cho 4 (3)
Từ (1) (2) và (3) => abc chia hết cho 60
T
1
1 tháng 9 2019
Giả sử trong ba số a,b,c không có số nào chia hết cho 3
Khi đó \(a=3k\pm1\left(k\in Z\right)\)
\(b=3l\pm1\left(l\in Z\right)\)
\(c=3m\pm1\left(m\in Z\right)\)
\(\Rightarrow a^3\)chia 9 dư 1 hoặc -1
\(b^3\)chia 9 dư 1 hoặc -1
\(c^3\)chia 9 dư 1 hoặc -1
TH1: Nếu a chia hết cho 9 dư 1; b chia 9 dư 1; c chia 9 dư 1
\(\Rightarrow a^3+b^3+c^3\)chia 9 dư 3( vô lý )
TH2: Nếu \(a^3\)chia 9 dư 1 ; \(b^3\)chia 9 dư 1 ; \(c^3\)chia 9 dư 1
\(\Rightarrow a^3+b^3+c^3\)chia 9 dư 1( vô lý )
TH3: Nếu \(a^3\)chia 9 dư 1; \(b^3\)chia 9 dư -1 ;\(c^3\)chia 9 dư -1
\(\Rightarrow a^3+b^3+c^3\)chia 9 dư -1( vô lý )
TH4: Nếu \(a^3\)chia 9 dư -1; \(b^3\)chia 9 dư -1 ;\(c^3\)chia 9 dư -1
\(\Rightarrow a^3+b^3+c^3\)chia 9 dư -3 ( vô lý )
Vì a,b,c vai trò như nhau nên điều giả sử sai
Vậy luôn tồn tại 1 trong 3 số chia hết cho 3
14 tháng 9 2021
a) Ta có:
\(n^2\left(n+1\right)-n\left(n+1\right)=n\left(n-1\right)\left(n+1\right)\)
Vì trong 3 số nguyên liên tiếp, có ít nhất 1 số chia hết cho 3 và 1 số chia hết cho 2 nên tích n(n-1)(n+1) chia hết cho 6 hay \(n^2\left(n+1\right)-n\left(n+1\right)\) chia hết cho 6(đpcm).
b) Ta có:
\(20^{n+1}-20^n=20^n\cdot19\)
Vì \(20^n\) là số nguyên nên \(20^n\cdot19⋮19\). Hay \(20^{n+1}-20^n⋮19\left(đpcm\right)\)
16 tháng 6 2015
ta có a: 3 dư 1( vì tổng các chữ số của a = 52 : 3 dư 1)
b: 3 dư 2( vì tổng các chữ số của b = 104 : 3 dư 2)
Đặt a = 3m+1, b=3n+2( m, n thuộc N)
có a.b =(3m+1)(3n+2)=3(3mn+2m+n) +2 : 3 dư 2
Vậy ab : 3 dư 2
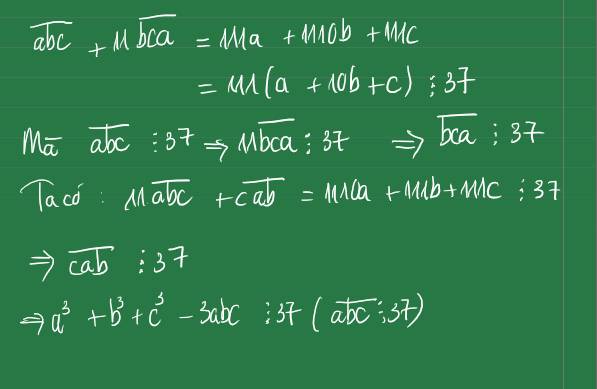
Ta có: \(\overline{abc}⋮37\Leftrightarrow100a+10b+c⋮37\)(1)
+) (1) => \(10\left(100a+10b+c\right)⋮37\)
<=> \(100b+10c+a+999a⋮37\) mà \(999a=37.27a⋮37\)
=> \(100b+10c+a⋮37\Leftrightarrow\overline{bca}⋮37\)
+) (1) => \(100\left(100a+10b+c\right)⋮37\)
<=> \(\left(100c+10a+b\right)+999\left(10a+b\right)⋮37\)mà \(999\left(10a+b\right)=37.27\left(10a+b\right)⋮37\)
=> \(\overline{cab}=100c+10a+b⋮37\)