Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
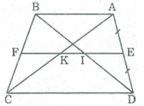
Xét hình thang ABCD có AB // CD.
E là trung điểm AD, đường thẳng đi qua E song song với AB cắt BC tại F, AC tại K, BD tại I.
Vì E là trung điểm AD nên EF// AB
Suy ra: BF = FC (tính chất đường trung bình hình thang)
Trong ∆ ADC ta có: E là trung, điểm của cạnh AD
EK // DC
Suy ra: AK = KC (tính chất đường trung bình của tam giác)
Trong ∆ ABD ta có: E là trung điểm của cạnh AD
EI // AB
Suy ra: BI = ID (tính chất đường trung bình của tam giác)
Vậy đường thẳng song song với 2 đáy, đi qua trung điểm E của cạnh bên AD của hình thang ABCD thì đi qua trung điểm của cạnh bên BC và trung điểm hai đường chéo AC, BD.
Giả sử hình thang là ABCD
trung điểm của cạnh AD là E
EF // AB // DC (F thuộc BC)
Gọi I là gia điểm AC , EF
Ta có
EI//DC (I thuộc EF , EF//DC)
EA=ED
=> EI là đường trung bình của tam giác ACD
=>AI=IC
Ta có
IF//AB (I thuộc EF,EF//AB)
AI=IC (cmt)
=> IF là đường trung bình của tam giác ABC
=>BF=FC
Gọi K là trung điểm BD và EF
ta có
BF=FC
KF//DC(K thuộc EF, EF//DC)
=>KF là đường trung bình của tam giác BDC
=>BK=KD
Xong rồi nha !!!!
1 T I C K nha
____________________________CHÚC BẠN HỌC TỐT _________________________
Vẽ hình thang ABCD, AB song song với CD. Lấy M, N lần lượt là trung điểm của BD và AC. Lấy H và K lần lượt là trung điểm của BC và AD.
Xét tam giác BCD có: - KB = KC (gt)
- MB = MD (gt)
MK là trung bình của BCD.
MK song song và bằng ½ CD
Tương tự như trên ta có:
- HN là trung bình ADC. HN song song và bằng ½ CD.
- HM là trung bình ABD. HM song song và bằng ½ AB.
- KN là trung bình của CAB. KN song song và bằng ½ AB.
H, M, N, K thẳng hàng (tiên đề Ơ – clit)
HK là trung bình của hình thang ABCD (tự chứng minh).
HK = (AB + CD)/2 (t/c)
HM + NK + KM + HN = 2HK.
mà MN = HK – HM – NK
MN = (HM + NK + KM + HN)/2 – HM – NK
= (AB + CD)/2 – AB
= 1/2AB – AB + CD/2
= CD/2 – 1/2AB
= (CD – AB)/2 (đpcm)