K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

19 tháng 4 2017
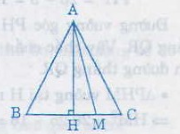
Giả sử ∆ABC cân tại A, M là điểm thuộc cạnh đáy BC, ta chứng minh AM ≤ AB;
AM ≤ AC
+ Nếu M ≡ A hoặc M ≡ B ( Kí hiệu đọc là trùng với) thì AM = AB, AM = AC.
+ Nếu M nằm giữa B và C; ( M ≢ B , C). Gọi H là trung điểm của BC, mà ∆ABC cân tại A nên AH ⊥ BC
+ Nếu M ≡ H => AM ⊥ BC => AM < AB và AM < AC
+ Nếu M ≢ K giả sử M nằm giữa H và C=> MH < CH
Vì MN và CH là hình chiếu MA và CA trên đường BC nên MA < CA => MA < BA
Chứng minh tương tự nếu M nằm giữa H và B thì MA < AB, MA < AC
Vậy mọi giá trị của M trên cạnh đáy BC thì AM ≤ AB, AM ≤ AC
Mình làm đúng đó
Đảm bảo 100%
nha
Nếu: \(\Delta ABC\)cân tại a, M là điểm thuộc cạnh đáy BC, ta chứng minh \(AM\le AB\), \(AM\le AC\)
+ Nếu M = A hoặc M = B ( kí hiệu đọc là trùng với ) thì AM = AB ư, AM = AC
+ Nếu M nằm giữa B và C; ( M \(\ne\)B, C ). Gọi H là trung điểm của BC, mà \(\Delta\)ABC cân tại a nên AH \(⊥\)BC
+ Nếu M = H \(\Rightarrow\)AM \(⊥\)BC \(\Rightarrow\)AM < AB và AM < AC
+ Nếu M \(\ne\)K giả sử M nằm giữa H và C \(\Rightarrow\)MH < CH
Vì MN và CH là hình chiếu MA và CA trên đường BC nên MA < CA \(\Rightarrow\)MA < BA
Chứng minh tương tự nếu M nằm giữa H và B thì MA < AB, MA < AC
Vậy mọi giá trị của M trên cạnh đáy BC thì AM \(\le\)AB, AM \(\le\)AC