
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đề bài không rõ ràng, em liên hệ người ra đề xem vẽ đồ thị đường thẳng nào? Vì đường thẳng đề cho có a chưa biết

1:
a: góc PAO+góc PBO=180 độ
=>PAOB nội tiếp
b: Xét (O) có
PA,PB là tiếp tuyến
=>PA=PB
mà OA=OB
nên OP là trung trực của AB
=>OP vuông góc AB
góc ABC=1/2*sđ cung AC=90 độ
=>BC//OP
cos AOP=OA/OP=1/2
=>góc AOP=60 độ
=>góc AOB=120 độ



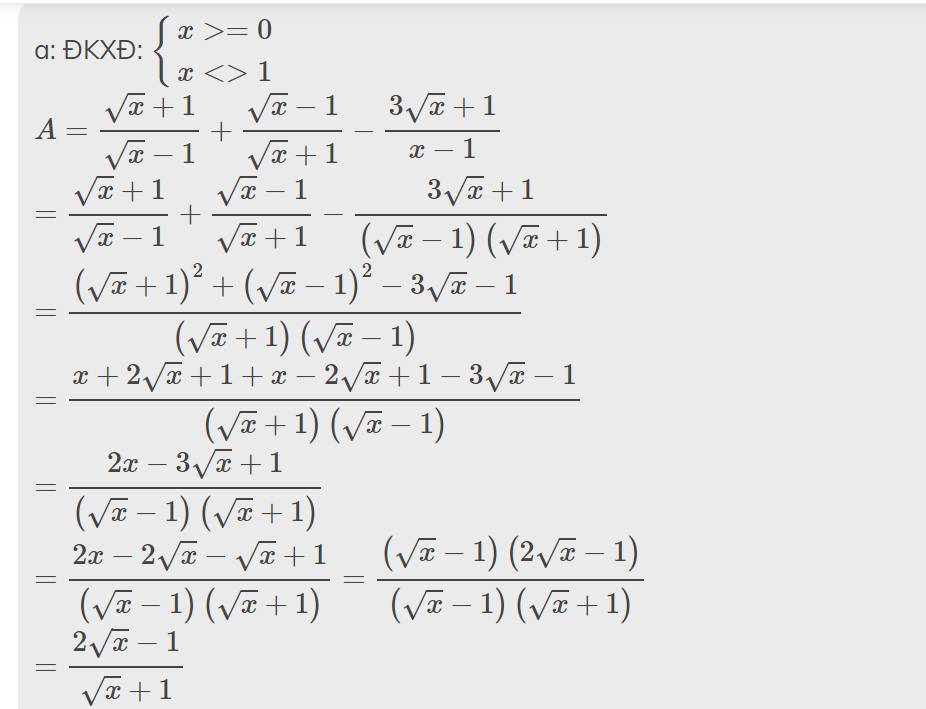
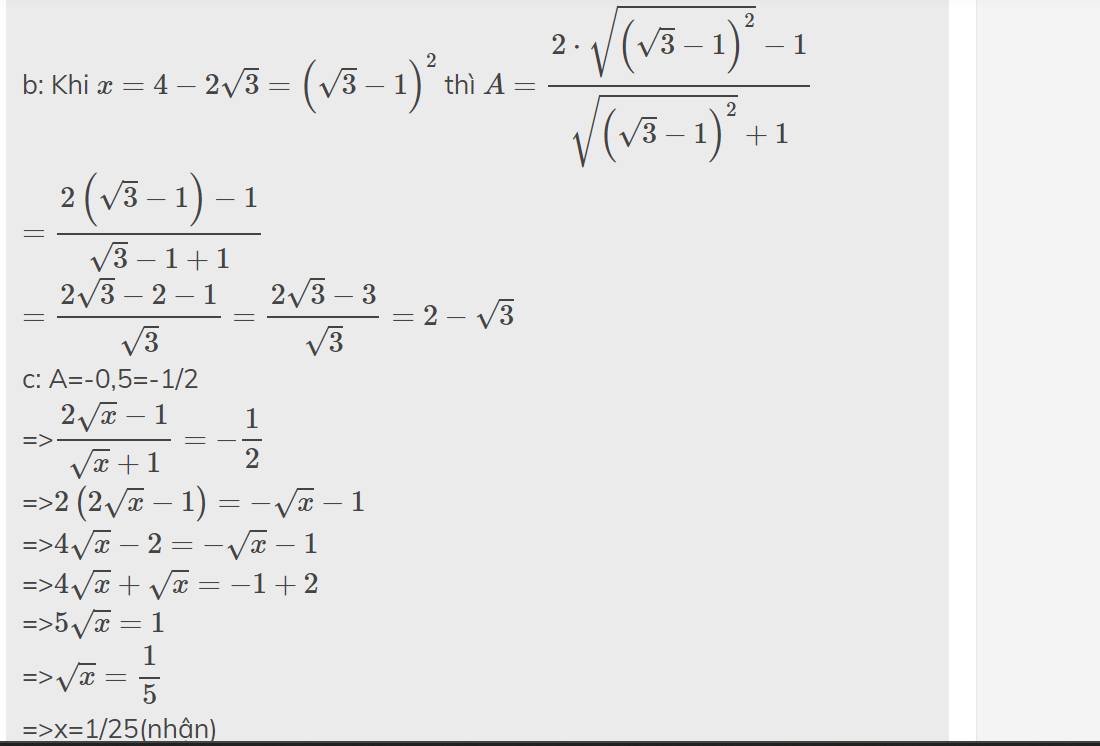

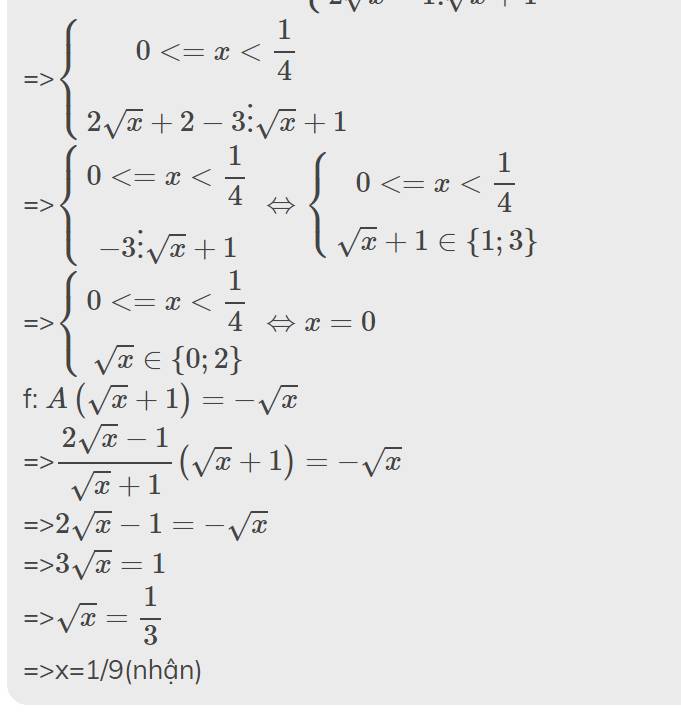
g: A<1
=>\(\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}< 1\)
=>\(\dfrac{2\sqrt{x}-1-\sqrt{x}-1}{\sqrt{x}+1}< 0\)
=>\(\sqrt{x}-2< 0\)
=>\(\sqrt{x}< 2\)
=>0<=x<4
Kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}0< =x< 4\\x< >1\end{matrix}\right.\)
h: \(A=\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}\)
=>\(A=\dfrac{2\sqrt{x}+2-3}{\sqrt{x}+1}=2-\dfrac{3}{\sqrt{x}+1}\)
\(\sqrt{x}+1>=1\forall x\) thỏa mãn ĐKXĐ
=>\(\dfrac{3}{\sqrt{x}+1}< =\dfrac{3}{1}=3\forall x\) thỏa mãn ĐKXĐ
=>\(-\dfrac{3}{\sqrt{x}+1}>=-3\forall x\) thỏa mãn ĐKXĐ
=>\(-\dfrac{3}{\sqrt{x}+1}+2>=-3+2=-1\forall x\) thỏa mãn ĐKXĐ
=>\(A>=-1\forall x\) thỏa mãn ĐKXĐ
Vậy: \(A_{min}=-1\) khi x=0
i: \(P=A\left(-x+2\sqrt{x}+3\right)\)
\(=\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}\cdot\left(-1\right)\cdot\left(x-2\sqrt{x}-3\right)\)
\(=\dfrac{1-2\sqrt{x}}{\sqrt{x}+1}\cdot\left(\sqrt{x}-3\right)\left(\sqrt{x}+1\right)\)
\(=\left(1-2\sqrt{x}\right)\left(\sqrt{x}-3\right)\)
\(=\sqrt{x}-3-2x+6\sqrt{x}=-2x+7\sqrt{x}-3\)
\(=-2\left(x-\dfrac{7}{2}\sqrt{x}+\dfrac{3}{2}\right)\)
\(=-2\left(x-2\cdot\sqrt{x}\cdot\dfrac{7}{4}+\dfrac{49}{16}-\dfrac{1}{16}\right)\)
\(=-2\left(\sqrt{x}-\dfrac{7}{4}\right)^2+\dfrac{1}{8}< =\dfrac{1}{8}\forall x\) thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi \(\sqrt{x}-\dfrac{7}{4}=0\)
=>\(\sqrt{x}=\dfrac{7}{4}\)
=>\(x=\dfrac{49}{16}\)

Đk: \(2\le x\le4\)
Áp dụng BĐT bunhiacopxki có:
\(P^2=\left(\sqrt{x-2}+3\sqrt{4-x}\right)^2\le\left(1+3^2\right)\left(x-2+4-x\right)\)
\(\Leftrightarrow P^2\le20\)\(\Leftrightarrow P\le2\sqrt{5}\)
Dấu "=" xảy ra khi \(\sqrt{x-2}=\dfrac{\sqrt{4-x}}{3}\) \(\Leftrightarrow x=\dfrac{11}{5}\) (tm đk)
Có \(P^2=8\left(4-x\right)+6\sqrt{\left(x-2\right)\left(4-x\right)}+2\ge2\)\(\Rightarrow P\ge\sqrt{2}\)
Dấu "=" xảy ra khi x=4 (tm)

1: Xét ΔMNP vuông tại M có MH là đường cao
nên MH^2=HN*HP; MN^2=NH*NP; PM^2=PH*PN
=>MH=căn 3,6*6,4=4,8cm; MN=căn 3,6*10=6cm; PM=căn 6,4*10=8cm
2: MK=8/2=4cm
Xét ΔMNK vuông tại M có tan MNK=MK/MN=4/6=2/3
nên \(\widehat{MNK}\simeq33^041'\)
3: ΔMNK vuông tại M có MF là đường cao
nên NF*NK=NM^2
ΔMNP vuông tại M có MH là đường cao
nên NH*NP=NM^2
=>NF*NK=NH*NP
 cíu lẹ ạ!
cíu lẹ ạ! cíu lẹ cíu lẹ
cíu lẹ cíu lẹ 

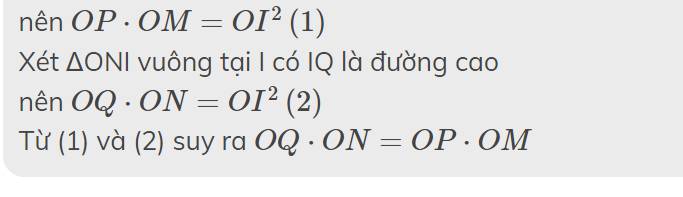



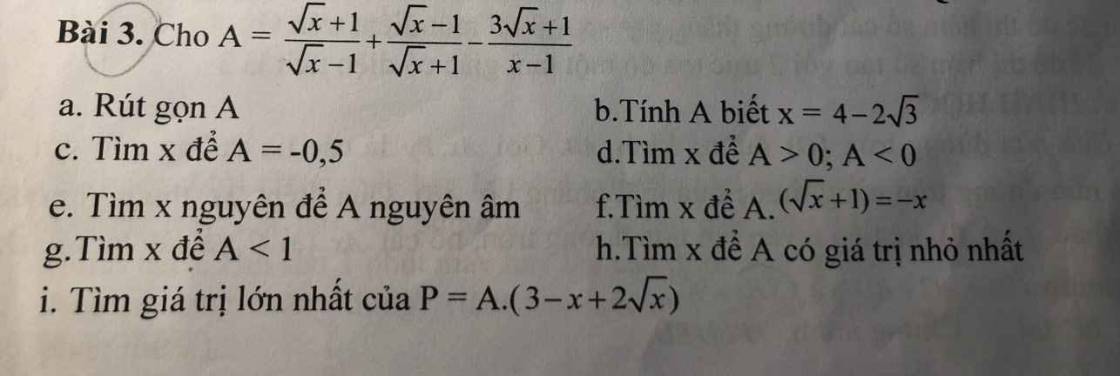 cíu cíu
cíu cíu cíu tui cíu tui
cíu tui cíu tui
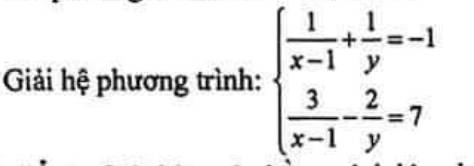
ĐKXĐ: x<>1 và y<>0
\(\left\{{}\begin{matrix}\dfrac{1}{x-1}+\dfrac{1}{y}=-1\\\dfrac{3}{x-1}-\dfrac{2}{y}=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{2}{x-1}+\dfrac{2}{y}=-2\\\dfrac{3}{x-1}-\dfrac{2}{y}=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{5}{x-1}=5\\\dfrac{1}{x-1}+\dfrac{1}{y}=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x-1=1\\\dfrac{1}{y}=-1-1=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=-\dfrac{1}{2}\end{matrix}\right.\left(nhận\right)\)