NA
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DM
2
HC
26 tháng 3 2017
Tk mình đi mọi người mình bị âm nè!
Ai tk mình mình tk lại cho!!
HC
26 tháng 3 2017
Tk mình đi mọi người mình bị âm nè!
Ai tk mình mình tk lại cho!!
HL
1
22 tháng 10 2019
Câu hỏi của phamvanquyettam - Toán lớp 6 - Học toán với OnlineMath
PD
1
NT
3
28 tháng 6 2016
Ta có: A = 4 + 22 + 23 + .... +220
2A = 8 + 23 + 24 + .......+221
=> 2A - A = 221 +8 - 4 - 22
=> A = 221 là 1 lũy thừa của 2 (Đpcm)
28 tháng 6 2016
A=4+22+23+............+220
A=2+2+22+23+............+220
2A=22+22+23+...+221
A=2A-A=(22+22+23+...+221)-(2+2+22+23+............+220)
A=221
20 tháng 12 2021
b: \(A=3\left(1+3+3^2\right)+...+3^{58}\left(1+3+3^2\right)\)
\(=13\left(3+...+3^{58}\right)⋮13\)
20 tháng 12 2021
\(a,\Leftrightarrow2A=8+2^3+2^4+...+2^{21}\\ \Leftrightarrow2A-A=8+2^3+2^4+...+2^{21}-4-2^2-2^3-...-2^{20}\\ \Leftrightarrow A=2^{21}+8-4-2^2=2^{21}\left(đpcm\right)\\ b,A=\left(3+3^2+3^3\right)+\left(3^4+3^5+3^6\right)+...+\left(3^{58}+3^{59}+3^{60}\right)\\ A=3\left(1+3+3^2\right)+3^4\left(1+3+3^2\right)+...+3^{58}\left(1+3+3^2\right)\\ A=\left(1+3+3^2\right)\left(3+3^4+...+3^{58}\right)\\ A=13\left(3+3^4+...+3^{58}\right)⋮13\)
PT
1
CM
10 tháng 3 2019
Ta có A = 2A – A = 2( 1 + 2 + 2 2 + 2 3 + . . . + 2 50 ) – ( 1 + 2 + 2 2 + 2 3 + . . . + 2 50 )
= 2 + 4 + 2 3 + 2 4 + . . . + 2 51 – ( 1 + 2 + 2 2 + 2 3 + . . . + 2 50 )
= 6 + 2 3 + 2 4 + . . . + 2 51 – ( 7 + 2 3 + . . . + 2 50 ) = 2 51 - 1
Suy ra : A + 1 = 2 51
Vậy A+1 là một lũy thừa của 2
PT
1
NA
3
2 tháng 11 2021
\(\Rightarrow2A=8+2^3+...+2^{2022}\\ \Rightarrow2A-A=8+2^3+...+2^{2022}-4-2^2-...-2^{2021}\\ \Rightarrow A=8+2^{2022}-4-2^2=8-4-4+2^{2022}=2^{2022}\left(đpcm\right)\)
2 tháng 11 2021
\(A=2^2+2^2+2^3+...+2^{2021}=2^3+2^4+...+2^{2021}=2^{2022}\left(đpcm\right)\)
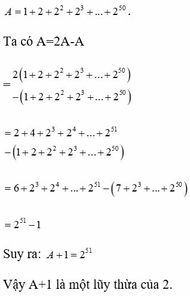
tách 4 = 22
8 = 23
típ tính 2A
Tìm 2A