Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABE vuông tại E và ΔACF vuông tại F có
AB=AC
\(\widehat{BAE}\) chung
Do đó: ΔABE=ΔACF
Suy ra: BE=CF và \(\widehat{ABE}=\widehat{ACF}\)
b: Xét ΔFBI vuông tại F và ΔECI vuông tại E có
FB=EC
\(\widehat{FBI}=\widehat{ECI}\)
Do đó: ΔFBI=ΔECI
Suy ra: IE=IF
c: Xét ΔAIB và ΔAIC có
AI chung
IB=IC
AB=AC
Do đó: ΔAIB=ΔAIC
Suy ra: \(\widehat{BAI}=\widehat{CAI}\)
hay AI là tia phân giác của góc A

ta có: a/b = 1/1/1 = 3/2 (1)
a - b = 8 (2)
từ (1) => 2a = 8b (nhân chéo nha)
=>a = 3b/a
thay a = 3b/a vào (2)
3b/2 - b = 8
giải tiếp nha
kết quả: a = 24
b = 16

Trước hết ta so sánh 10A và 10B
Ta có:
\(10A=\frac{10^{16}+10}{10^{16}+1}=1+\frac{9}{10^{16}+1}\) \(10B=\frac{10^{17}+10}{10^{17}+1}=1+\frac{9}{10^{17}+1}\)
Vì: \(\frac{9}{10^{16}+1}>\frac{9}{10^{17}+1}\) nên 10A > 10B, do đó A>B
Ta thấy:B<1 vì 1015+1<1016+1
Theo quy tắc :\(\frac{a}{b}\)<\(\frac{a+m}{b+m}\)nên ta có: B =\(\frac{10^{16}+1}{10^{17}+1}\)<\(\frac{10^{16}+1+9}{10^{17}+1+9}\)<\(\frac{10^{16}+10}{10^{17}+10}\)<\(\frac{10\left(10^{15}+1\right)}{10\left(10^{16}+1\right)}\)=A
Suy ra B<A

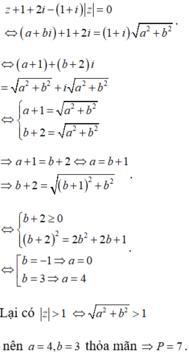
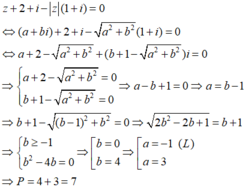
viết đề = fx đi khó hỉu quá