
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
MA
2

Các câu hỏi dưới đây có thể giống với câu hỏi trên
LM
0

DH
3

7 tháng 11 2023
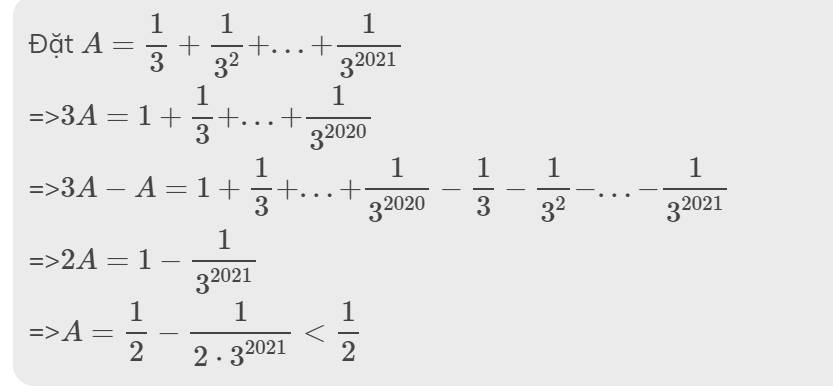
Đặt \(A=\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{2021}}\)
=>\(3A=1+\dfrac{1}{3}+...+\dfrac{1}{3^{2020}}\)
=>\(3A-A=1+\dfrac{1}{3}+...+\dfrac{1}{3^{2020}}-\dfrac{1}{3}-\dfrac{1}{3^2}-...-\dfrac{1}{3^{2021}}\)
=>\(2A=1-\dfrac{1}{3^{2021}}\)
=>\(A=\dfrac{1}{2}-\dfrac{1}{2\cdot3^{2021}}< \dfrac{1}{2}\)

10 tháng 8 2016
bn da hoc so thap phan vo han tuan hoan chua ? mk c/m nhe
a) 0,(37) + 0,(62) = 0,(99) = 99/99 =1 (dpcm)
b) 0,33 .3 = 0,99 khác 1 bn à
Ta có \(\dfrac{1}{3^3}< \dfrac{1}{2.3.4}=\dfrac{1}{2}\left(\dfrac{1}{2.3}-\dfrac{1}{3.4}\right)\)
\(\dfrac{1}{5^3}< \dfrac{1}{4.5.6}=\dfrac{1}{2}\left(\dfrac{1}{4.5}-\dfrac{1}{5.6}\right)\\ ...\\ \dfrac{1}{2021^3}< \dfrac{1}{2020.2021.2022}=\dfrac{1}{2}\left(\dfrac{1}{2020.2021}-\dfrac{1}{2021.2022}\right)\)
Cộng VTV ta được
\(VT< \dfrac{1}{2}\left(\dfrac{1}{2.3}-\dfrac{1}{2021.2022}\right)=\dfrac{1}{12}-\dfrac{1}{2\left(2021.2022\right)}< \dfrac{1}{12}\)
\(n^3=n.n^2>n\left(n^2-1\right)=\left(n-1\right)n\left(n+1\right)\)
\(\dfrac{1}{n^3}< \dfrac{1}{\left(n-1\right)n\left(n+1\right)}\)
\(\dfrac{1}{\left(n-1\right)n\left(n+1\right)}=\dfrac{1}{2}.\dfrac{n+1-\left(n-1\right)}{\left(n-1\right)n\left(n+1\right)}=\dfrac{1}{2}\left(\dfrac{1}{\left(n-1\right)n}-\dfrac{1}{n\left(n+1\right)}\right)\)
\(\dfrac{1}{3^3}+\dfrac{1}{5^3}+.......+\dfrac{1}{2009^3}< \dfrac{1}{2.3.4}+\dfrac{1}{3.4.5}+.....\dfrac{1}{2008.2009.2010}=\dfrac{1}{2}\left(\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{3.4}-\dfrac{1}{4.5}+.........+\dfrac{1}{2008.2009}-\dfrac{1}{2009.2010}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{1}{2.3}-\dfrac{1}{2009.2010}\right)\)
\(=\dfrac{1}{2}\)