NH
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
T
1
28 tháng 4 2020
F(x) = x2 + 5x - 3
F(-2) = (-2)2 + 5(-2) - 3 = 4 - 10 - 3 = -9 \(\ne\) 0
Vậy x = -2 không phải nghiệm của đa thức F(2) = x2 + 5x - 3
Chúc bn học tốt!
S
2
3 tháng 8 2018
\(2x^2+8x+17=2.\left(x^2+2.x.2+2^2\right)+9=2.\left(x+2\right)^2+9\)
Ta có: \(2.\left(x+2\right)^2\ge0\forall x\)
\(\Rightarrow2.\left(x+2\right)^2+9\ge9\forall x\)
\(\Rightarrow2x^2+8x+17>0\forall x\)
\(\Rightarrow\)đa thức \(2x^2+8x+17\)vô nghiệm
đpcm
\(-x^2+4x-6=-\left(x^2+2.x.2+2^2\right)-2=-\left(x+2\right)^2-2\)
Ta có:\(\left(x+2\right)^2\ge0\forall x\)
\(\Rightarrow-\left(x+2\right)^2\le0\forall x\)
\(\Rightarrow-\left(x+2\right)^2-2\le-2\forall x\)
\(\Rightarrow-\left(x+2\right)^2-2< 0\forall x\)
\(\Rightarrow\)đa thức \(-x^2+4x-6\)vô nghiệm
đpcm
Tham khảo nhé~
K
1
HT
0
S
24 tháng 4 2023
\(Q\left(x\right)=-3x^4+4x^3+2x^2+\dfrac{2}{3}-3x-2x^4-4x^3+8x^4+1+3x\)
\(=\left(-3x^4-2x^4+8x^4\right)+\left(4x^3-4x^3\right)+2x^2-\left(3x-3x\right)+\left(1+\dfrac{2}{3}\right)\)
\(=3x^4+2x^2+\dfrac{5}{3}\)
\(3x^4+2x^2+\dfrac{5}{3}=0\)
\(\Rightarrow3x^4+2x^2=-\dfrac{5}{3}\)(Vô lí vì \(3x^4\) và \(2x^2\) luôn lớn hơn hoặc bằng 0)
Vậy Q(x) không có nghiệm
24 tháng 4 2023
Q(x)=3x^4+2x^2+5/3>=5/3>0 với mọi x
=>Q(x) vô nghiệm
TU
1
21 tháng 4 2020
Ta có: P(x) = 2 . ( x2 + 4x ) + 17
= 2 . ( x2 + 2 . x . 2 + 22 - 22 ) + 17
= 2 . [ ( x2 + 2 . x . 2 + 22 ) - 22 ] + 17
= 2 . [ ( x + 2 )2 - 4 ] + 17
= 2 . ( x + 2 )2 - 8 + 17
= 2 . ( x + 2 )2 + 9
Vì ( x + 2 )2 \(\ge\) 0 với mọi x
\(\Rightarrow\) 2 . ( x + 2 )2 \(\ge\) 0 với mọi x
\(\Rightarrow\) 2 . ( x + 2 )2 + 9 \(\ge\) 9 \(>\) 0 với mọi x
\(\Rightarrow\) P(x) \(\ge\) 0 với mọi x
\(\Rightarrow\)Đa thức P(x) không có nghiệm
MK
1
6 tháng 5 2016
x^2+8x+19
=x^2+4x+4x+8+11
=(x^2-4x)-(4x-8)+11
=x(x-4)-(x-4)+11
=(x-4)-(x-4)+11
=(x-4)^2+11
Vì (x-4)^2 Lớn hơn hoặc bằng 0
=>(x-4)^2+11>0
Vậy đa thức sau không có nghiệm
PT
2
CM
10 tháng 2 2019
Ta có:
Nhận xét : Với mọi số thực y ta có : y4 = (y2)2 ≥ 0 ⇒ y4 + 2 ≥ 2 > 0.
Vậy với mọi số thực y thì Q(y) > 0 nên không có giá trị nào của y để Q(y) = 0 hay đa thức vô nghiệm.
HT
1
29 tháng 4 2022
Vì \(\left(x-3\right)^2\ge0\Rightarrow\left(x-3\right)^2+1>0\)
Vậy pt vô nghiệm
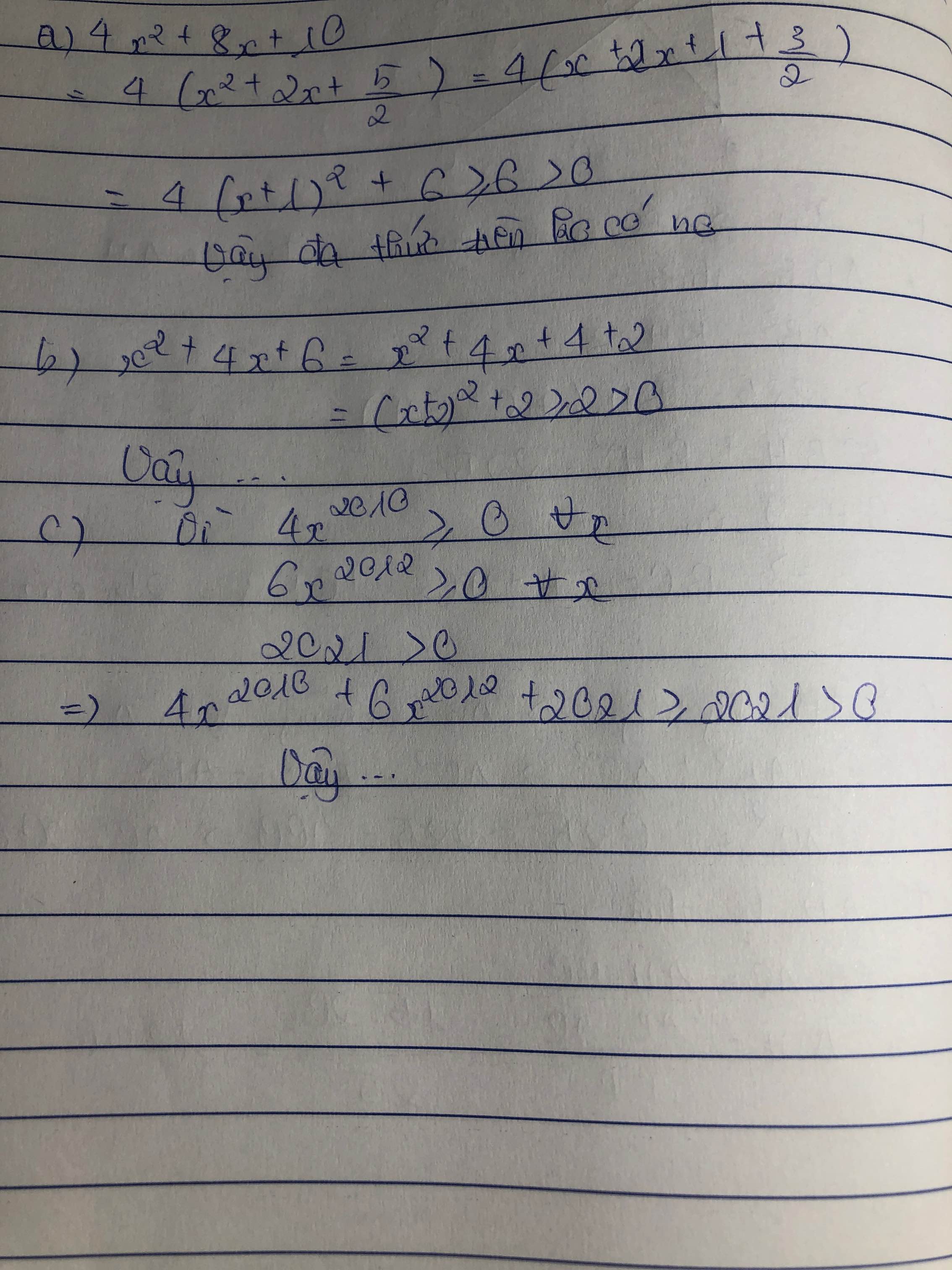
8x - x2 - 17 = - (x2 -8x + 16) - 1 = -(x-4)2 - 1
-(x-4)2 ≤ 0 ; ⇔ -(x-4)2 ≤ -1 < 0 ∀ x vậy đa thức ko có nghiệm