Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:

Chứng minh định lý hàm cos
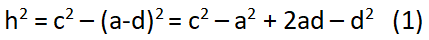
Chứng minh định lý hàm cos – Phương trình 1
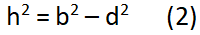
Chứng minh định lý hàm cos – Phương trình 2

Chứng minh định lý hàm cos – Phương trình 3
Với d = b cosC thế vào phương trình biến đổi (3) ta rút ra điều phải chứng minh!

Câu hỏi của lê thị thu huyền - Toán lớp 9 - Học toán với OnlineMath

A H B C
kẻ CH vuông góc AB
Ta có : \(\sin A=\frac{CH}{AC};\sin B=\frac{CH}{BC}\)
do đó : \(\frac{\sin A}{\sin B}=\frac{BC}{AC}=\frac{a}{b}\Rightarrow\frac{a}{\sin A}=\frac{b}{\sin B}\)( 1 )
Tương tự : \(\frac{b}{\sin B}=\frac{c}{\sin C}\) ( 2 )
Từ ( 1 ) và ( 2 ) suy ra \(\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}\)

H A B C
a)Kẻ đường cao : BH , AI , CK
Ta có: sinA = BH / c ; sinB = AI / c
=> sinA/sinB = BH / AI ﴾1﴿
Mà BH = a.sinC ; AI = b.sinC
=> BH/AI = a/b ﴾2﴿
Từ ﴾1﴿ và ﴾2﴿ suy ra sinA/sinB = a/b => a/sinA = b/sinB
Bạn chỉ việc nói chứng minh tượng tự , ta có:
b/sinB = c/sinC ; c/sinC = a/sinA
Từ đó suy ra a /sinA = b / sinB = c /sinC
Chúc bạn học tốt
NHỚ TK MK NHA

a) Ta có: \(bc.sinA=ca.sinB=ab.sinC\left(=2S_{ABC}\right)\Rightarrow b.sinA=a.sinB;c.sinB=b.sinC\Rightarrow\frac{a}{sinA}=\frac{b}{sinB};\frac{b}{sinB}=\frac{c}{sinC}\Rightarrowđpcm\)
b) Ta có: \(a+b=2c\Leftrightarrow\frac{a}{c}+\frac{b}{c}=2\).
Từ câu a ta suy ra \(\frac{a}{c}=\frac{sinA}{sinC};\frac{b}{c}=\frac{sinB}{sinC}\).
Do đó: \(\frac{sinA}{sinC}+\frac{sinB}{sinC}=2\Rightarrow sinA+sinB=2sinC\) (đpcm).
A B C A' C' B' H a b c
\(AA'=c.sinB=b.sinC\Leftrightarrow\frac{c}{sinC}=\frac{b}{sinB}.\)
va\(BB'=c.sinA=a.sinC\Leftrightarrow\frac{c}{sinC}=\frac{a}{sinA}\)
\(\Leftrightarrow\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}\)
\(S_{\Delta ABC}=\frac{1}{2}.a.AA'=\frac{1}{2}.a.bsinC\)