Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử CD là một dây của đường tròn bán kính R và AB là một đường kính của nó. Ta có:
- Nếu C, O, D không thẳng hàng thì trong tam giác COD có
CD < OC + OD = 2R = AB.
- Nếu C, O, D thằng hàng thì
CD < OC + OD = R + R = 2R (1)
Do AB là đường kính nên: AB = 2R (2)
Từ (1) và (2) suy ra: CD < AB .
Vậy trong mọi trường hợp ta luôn có đường kính là dây lớn nhất.

+) Ta có:
AC=AB=>^AC=^AB
^ACD=^ABD
^CD=^BP=>^CDA=^BAD hay ^IAC=IAB(1)
+) Ta có:
Đường tròn I=Đường tròn K (Vì chung R=1,5 cm)
Cung AB của đường tròn K
=>DB=DE
=>^IAB=^KAB(2)
Từ (1) và (2) suy ra:
^IAC=^IAB=^KAB

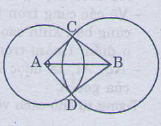
B1: Lần lượt lấy A và B làm tâm, ta quay hai cung tròn với bán kính R( Lưu ý R>1/2AB) Hai cung tròn (A;r) và (B;r) cắt nhay tại hai điểm M và M' b2: Nối MM' ta được đường trung trực MM' của đoạn thẳng AB.

∆BAC và ∆ BAD có: AC=AD(gt)
BC=BD(gt)
AB cạnh chung.
Nên ∆ BAC= ∆ BAD(c.c.c)
Suy ra ˆBACBAC^ = ˆBADBAD^(góc tương ứng)
Vậy AB là tia phân giác của góc CAD
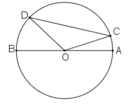
Giả sử ta có đường tròn tâm O đường kính AB, dây CD khác với đường kính
Vì O,C,D không thẳng hàng
nên DC<OC+OD=2R=AB
=>AB là dây lớn nhất