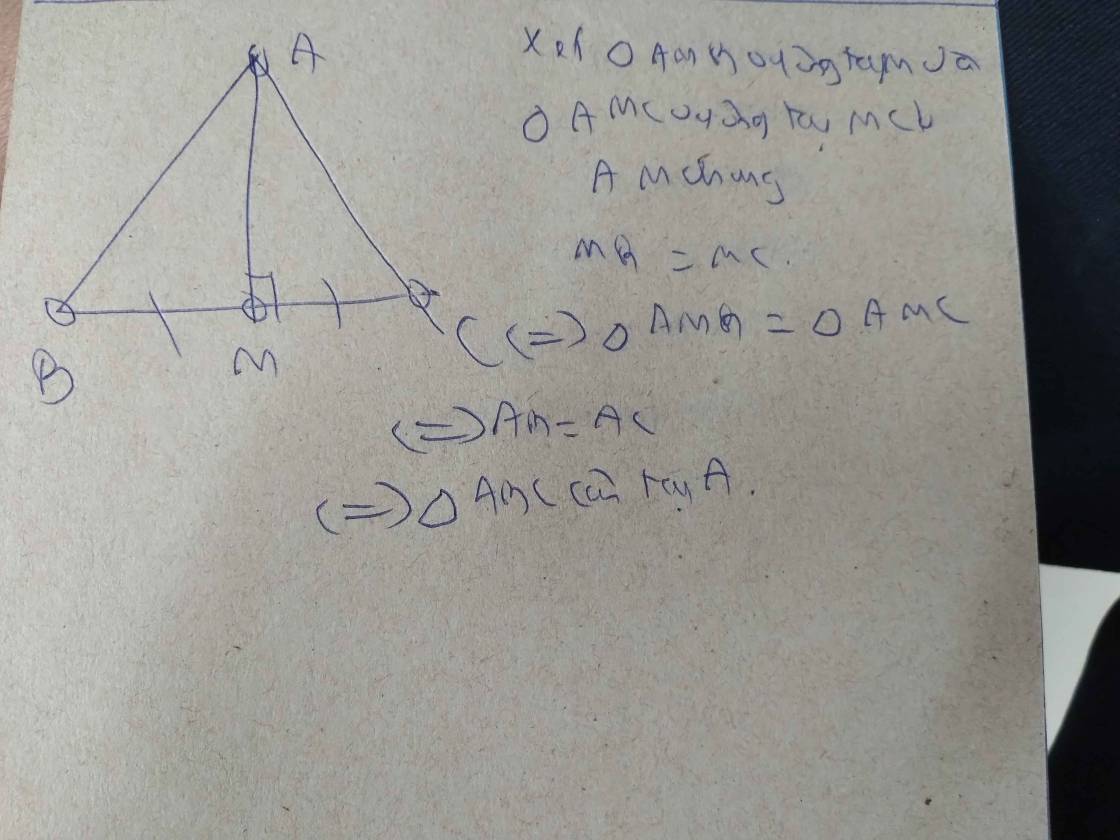Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trường hợp 1: ΔABC không cân
=>AM>AH(ΔAHM vuông tại H)
Trường hợp 2: ΔABC cân tại A
=>M trùng với H
=>AM=AH
Do đó: AM>=AH
Chứng minh rằng trong một tam giác, đường cao không lớn hơn đường trung tuyến xuất phát từ một đỉnh.

+) Xét tam giác có đường cao và đường trung tuyến cùng xuất phát từ cùng 1 đỉnh và không trùng nhau :
Vì đường cao và đường trung tuyến xuất phát từ cùng một đỉnh lần lươt là đường vuông góc và đường xiên kẻ từ cùng một điểm đến cùng một đường thẳng.
Do đó,đường cao nhỏ hơn đường trung tuyến (1)
+) Xét tam giác cân có đường cao và đường trung tuyến cùng xuất phát từ đỉnh của tam giác cân nên chúng bằng nhau (2)
Từ (1) và (2) suy ra: trong tam giác cân, đường cao không lớn hơn đường trung tuyến xuất phát từ cùng 1 đỉnh.

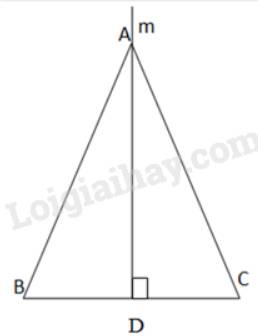
Từ A kẻ đường thẳng m vuông góc với BC tại trung điểm D của BC.
\( \Rightarrow \) AD là đường trung tuyến của BC.
Xét \(\Delta ABD\) và \(\Delta ACD\) có:
\(\begin{array}{l}\widehat {ADB} = \widehat {ADC} = {90^0}\\AD:chung\\BD = CD\left( {gt} \right)\\ \Rightarrow \Delta ABD = \Delta ACD\left( {c - g - c} \right)\end{array}\)
\( \Rightarrow AB = AC\)(2 cạnh tương ứng)
\( \Rightarrow \Delta ABC\)cân tại A (đpcm).

bạn tham khảo link này nha:https://hoc24.vn/hoi-dap/tim-kiem?id=137279&q=Ch%E1%BB%A9ng%20minh%20%3A%20trong%20m%E1%BB%99t%20tam%20gi%C3%A1c%20c%C3%A2n%2C%20%C4%91%C6%B0%E1%BB%9Dng%20ph%C3%A2n%20gi%C3%A1c%20xu%E1%BA%A5t%20ph%C3%A1t%20t%E1%BB%AB%20%C4%91%E1%BB%89nh%20%C4%91%E1%BB%93ng%20th%E1%BB%9Di%20l%C3%A0%20%C4%91%C6%B0%E1%BB%9Dng%20trung%20tuy%E1%BA%BFn%20%E1%BB%A9ng%20v%E1%BB%9Bi%20c%E1%BA%A1nh%20%C4%91%C3%A1y.

A B C M
Giả sử \(\Delta ABC\)cân tại A có AM là trung tuyến .
Xét \(\Delta AMB\)và \(\Delta AMC\)có :
AB = AC ( gt )
AM ( cạnh chung )
BM = CM ( gt )
Suy ra : \(\Delta AMB\)= \(\Delta AMC\)( c.c.c )
\(\Rightarrow\widehat{BAM}=\widehat{CAM}\)
Từ đó suy ra ; AM là tia phân giác của \(\Delta ABC\)