Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

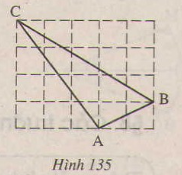
Gọi độ dài cạnh của mỗi ô vuông là 1.
Theo định lí Py-ta-go:
AB2 = 12 + 22 = 1 + 4 = 5
BC2 = 12 + 22 = 1 + 4 = 5
AC2 = 12 + 32 = 1 + 9 = 10
Do AB2 = BC2 nên AB = BC
Do AB2 + BC2 = AC2 nên \(\widehat{ABC}=90^o\)
Vậy \(\Delta ABC\) vuông cân tại B.

Xét tam giác ABC trên hình vẽ ta có:
AB = AC = 6 ô vuông (với điều kiện tất cả ô vuông đều bằng nhau).
=> Tam giác ABC là tam giác cân và cân tại A.


Ta có: AB2=AM2+MB2
=22+12=5
Nên AB= √5
AC2=AN2+NC2
=9+16=52
nên AC=5
BC2=BK2+KC2
= 32+52=9+25=34
BC= √34
Giải:
Ta có: AB2=AM2+MB2
=22+12=5
Nên AB= √5
AC2=AN2+NC2
=9+16=52
nên AC=5
BC2=BK2+KC2
= 32+52=9+25=34
BC= √34

Hướng dẫn :
Gọi M là giao điểm của hai tia phân giác của hai góc ngoài B và C của ∆ABC
Kẻ MH ⊥ AB; MI ⊥ BC; MK ⊥ AC
( H ∈ AB, I ∈ BC, K ∈ AC)
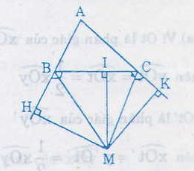
Ta có: MH = MI (Vì M thuộc phân giác của góc B ngoài)
MI = MK (Vì M thuộc phân giác của góc C ngoài)
Suy ra : MH = MK
=> M thuộc phân giác của góc ˆBACBAC^
Gọi M là giao điểm của hai tia phân giác của hai góc ngoài B và C của ∆ABC
Kẻ MH ⊥ AB; MI ⊥ BC; MK ⊥ AC
( H ∈ AB, I ∈ BC, K ∈ AC)

Ta có: MH = MI (Vì M thuộc phân giác của góc B ngoài)
MI = MK (Vì M thuộc phân giác của góc C ngoài)
Suy ra : MH = MK
=> M thuộc phân giác của gócA

Chứng minh tam giác vuông:
Ứng dụng:
- Vẽ đường tròn (A, r) với r = AB/2; vẽ đường tròn (B, r).
- Gọi C là giao điểm của hai cung tròn nằm ở phía trong tờ giấy.
- Trên tia BC lấy D sao cho BC = CD => AB ⊥ AD.
Thật vậy: ΔABD có AC là trung tuyến ứng với BD (BC = CD) và AC = BC = CD.
=> AC = BD => ∆ABD vuông tại A.


a,
Theo bài ra ta có:
+)FE//BC
+)EC//BA hay ED//BA
+)AC//FB hay AC//FD
Khi đó:
+)\(\widehat{FBA}=\widehat{BAC}\)
+)\(\widehat{B\text{AF}}=\widehat{ABC}\)
Vì BF//AC
Xét \(\Delta FBA\) và \(\Delta CAB\) có:
\(\left\{{}\begin{matrix}\widehat{B\text{AF}}=\widehat{ABC}\\BAchung\\\widehat{FBA}=\widehat{BAC}\end{matrix}\right.\) (cmt)
=> \(\Delta FBA\) = \(\Delta CAB\) (g.c.g)
=> FB=AC ( hai cạnh tương ứng )
Ta lại có:
+) \(\widehat{FAB}=\widehat{CEA}\)
+) \(\widehat{BFA}=\widehat{CAE}\)
( vì BF//CA và BA//CE )
=> \(\widehat{FBA}=\widehat{ACE}\)
Xét \(\Delta FBA\) và \(\Delta ACE\) có:
\(\left\{{}\begin{matrix}\widehat{BFA}=\widehat{CAE}\\FB=AC\\\widehat{FBA}=\widehat{ACE}\end{matrix}\right.\) (cmt)
=> \(\Delta FBA=\Delta ACE\left(g.c.g\right)\)
=> FA=EA ( hai cạnh tương ứng )
Mà F;A;E thẳng hàng
=> A là trung điểm của EF
(đ.p.c.m)
b,
Các đường cao của tam giác ABC là các đường trung trực của tam giác DFE
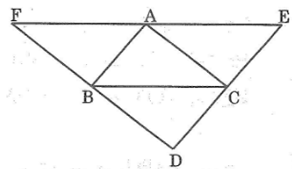
Xét ΔABC và ΔACE, ta có:
∠(ACB) = ∠(CAE) (so le trong, AE // BC)
AC cạnh chung
∠(CAB) = ∠(ACE) (so le trong, CE // AB)
Suy ra: ΔABC = ΔACE (g.c.g)
⇒ AE = BC (1)
Xét ΔABC và ΔABF, ta có:
∠(ABC) = ∠(BAF) (so le trong, AF // BC)
AB cạnh chung
∠(BAC) = ∠(ABF) (so le trong, BF // AC)
Suy ra: ΔABC = ΔBAF (g.c.g)
⇒ AF = BC (2)
Từ (1) và (2) suy ra: AE = AF
Vậy A là trung điểm của EF.
b. Kẻ AH ⊥ BC.
Ta có: EF // BC (gt) ⇒ AH ⊥ EF
Lại có: AE = AF (chứng minh trên)
Vậy đường cao AH là đường trung trực của EF.
Vì B là trung điểm DF và DF // AC nên đường cao kẻ từ đỉnh B của ΔABC là đường trung trực DF.
Vì C là trung điểm DE và DE // AB nên đường cao kẻ từ đỉnh C của ΔABC là đường trung trực của DE.
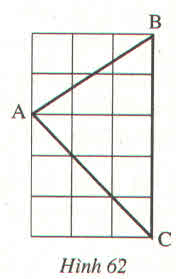

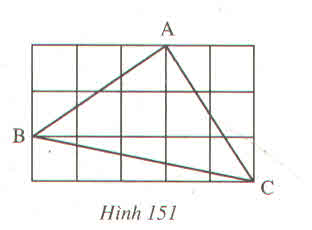
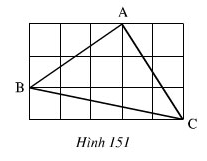
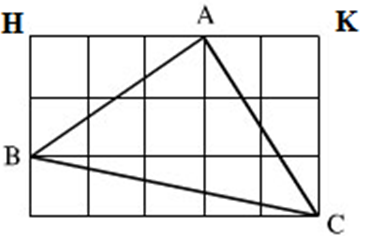
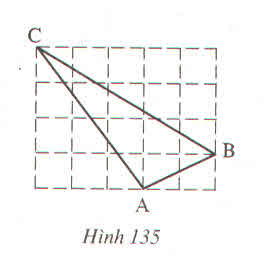
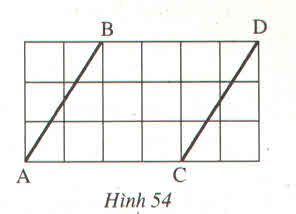



Giả sử độ dài mỗi ô vuông nhỏ là 1
Đường chéo mỗi ô vuông là Căn 2.
Độ dài các cạnh AB, AC, BC lần lượt là: ( căn 13) , 3 căn 2, 5
Ta thấy 3 cạnh không bằng nhau nên không phải tam giác đều.
Thử định lý pytago đảo không đúng nên không phải tam giác vuông.
So sánh tỉ lện giữ cách cạnh đều nhỏ hơn 2. Nên trong tam giác không có góc tù. Vậy tam giác là tam giác nhọn