Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác BFED có
ED//BF
FE//BD
Do đó: BFED là hình bình hành
Xét ΔABC có
D là trung điểm của BC
DE//AB
Do đó: E là trung điểm của AC
Xét ΔABC có
E là trung điểm của AC
EF//CB
Do đó: F là trung điểm của AB
Xét ΔCDE và ΔEFA có
CD=EF
DE=FA
CE=EA
Do đó: ΔCDE=ΔEFA
b: Gọi ΔABC có F là trung điểm của AB,E là trung điểm của AC
Trên tia FE lấy điểm E sao cho E là trung điểm của FK
Xét tứ giác AFCK có
E là trung điểm của AC
E là trung điểm của FK
Do đó: AFCK là hình bình hành
Suy ra: AF//KC và KC=AF
hay KC//FB và KC=FB
Xét tứ giác BFKC có
KC//FB
KC=FB
Do đó: BFKC là hình bình hành
Suy ra: FE//BC(ĐPCM)

a) Giả sử ∆ABC vuông góc tại A. Vẽ hai đường trung trực của hai cạnh góc vuông AB, AC cắt nhau tại M. Ta chứng minh M là trung điểm của BC.

Vì M là giao điểm hai đường trung trực d1, d2
của AB, AC mà AB ⊥ AC nên B, M, C thẳng hàng (bài tập 55)
Vì MA = MB (M thuộc đường trung trực của AB)
MA = MC (M thuộc đường trung trực của AC)
=> MB = MC
Do B, M, C thẳng hàng và M cách đều BC nên M là trung điểm của BC
b) M là trung điểm Bc => MB = 1212 BC
mà AM = MB nên MA =1212 BC
Vậy độ dài đường trung tuyến xuất phát từ đỉnh góc vuông bằng một nửa độ dài cạnh huyền.
a) Giả sử ∆ABC vuông góc tại A. Vẽ hai đường trung trực của hai cạnh góc vuông AB, AC cắt nhau tại M. Ta chứng minh M là trung điểm của BC.

Vì M là giao điểm hai đường trung trực d1, d2
của AB, AC mà AB ⊥ AC nên B, M, C thẳng hàng (bài tập 55)
Vì MA = MB (M thuộc đường trung trực của AB)
MA = MC (M thuộc đường trung trực của AC)
=> MB = MC
Do B, M, C thẳng hàng và M cách đều BC nên M là trung điểm của BC
b) M là trung điểm Bc => MB = 1212 BC
mà AM = MB nên MA =1212 BC
Vậy độ dài đường trung tuyến xuất phát từ đỉnh góc vuông bằng một nửa độ dài cạnh huyền

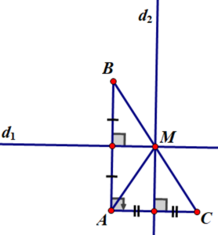
+ Giả sử ∆ABC vuông tại A.
d1 là đường trung trực cạnh AB, d2 là đường trung trực cạnh AC.
d1 cắt d2 tại M. Khi đó M là điểm cách đều ba đỉnh của tam giác ABC.
+ Áp dụng kết quả bài 55 ta có B, M, C thẳng hàng.
+ M cách đều A, B, C ⇒ MB = MC ⇒ M là trung điểm của cạnh BC (đpcm)
+ M là trung điểm của cạnh BC (đpcm)
*) Giả sử AM là trung tuyến của tam giác ABC suy ra M là trung điểm của cạnh BC
⇒ MB = MC = BC/2
Mà MA = MB = MC (cmt)
⇒ MA = BC/2
Vậy độ dài đường trung tuyến xuất phát từ đỉnh góc vuông bằng một nửa độ dài cạnh huyền.

a) Giả sử ∆ABC vuông góc tại A. Vẽ hai đường trung trực của hai cạnh góc vuông AB, AC cắt nhau tại M. Ta chứng minh M là trung điểm của BC.

Vì M là giao điểm hai đường trung trực d1, d2
của AB, AC mà AB ⊥ AC nên B, M, C thẳng hàng (bài tập 55)
Vì MA = MB (M thuộc đường trung trực của AB)
MA = MC (M thuộc đường trung trực của AC)
=> MB = MC
Do B, M, C thẳng hàng và M cách đều BC nên M là trung điểm của BC
b) M là trung điểm Bc => MB = BC
mà AM = MB nên MA = BC
Vậy độ dài đường trung tuyến xuất phát từ đỉnh góc vuông bằng một nửa độ dài cạnh huyền.

http://cdn.powergatevn.com/Stas/Images/2014/8/29/HA622u0e.jpg
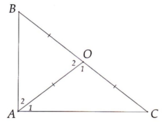
Xét tam giác ABC vuông tại A
Vẽ đường trung trực d1 của cạnh AB, cắt AB tại I
vẽ đường trung trực d2 của cạnh AC, cắt AC tại H
Giả sử d1 và d2 cắt nhau tại O. Ta có OA = OB ; OA = OC (t/c đường trung trực)
Xét 2 tam giác vuông OAI và OBI có:
OA = OB (cmt)
IO chung
=> Tam giác OAI = tam giác OBI (cạnh huyền - cạnh góc vuông)
=> IA = IB (2 cạnh tương ứng) => IO là đường trung tuyến
Xét 2 tam giác vuông OAH và OCH có:
OA = OC (cmt)
HO chung
=> Tam giác OAH = tam giác OCH (cạnh huyền - cạnh góc vuông)
=> IA = IC (2 cạnh tương ứng) => OH là đường trung tuyến
mà OH và OI giao nhau tại 1 điểm O => O là trọng tâm
nên OA là đường trung tuyến => Điều phải chứng minh

Vì tâm đường tròn đi qua 3 đỉnh của tam giác với mỗi tam giác chỉ có duy nhất 1 điểm.
Gọi I là trung điểm cạnh huyển BC của tam giác ABC vuông tại A.
Ta sẽ đi chứng minh I là tâm đường tròn đi qua 3 đỉnh tam giác ABC.
Thật vậy, trên tia đối tia IA , ta lấy điểm D sao cho IA=ID .
Vì I là trung điểm BC => IB=IC
Xét tam giác AIB và tam giác CID có:
AI=IC ; BI=ID ; AIB =CID (2 góc đối đỉnh)
=> Tam giác AIB =tam giác CID (c.g.c)
=> AB=CD; IAB = ICD
Vì IAB =ICD , mà 2 góc này ở vị trí so le trong
=> AB// CD Mà AB vuông góc với AC
=> CD vuông góc AC => ACD = 90
Xét tam giác BAC và DCA có:
AC chung ; AB=DC ; BAC = DCA =90
=> BAC = DCA(c.g.c)
=> BC = DA
Mà IB = IC = BC/2; AI=ID =DA/2
=> IB=IC=IA
=> I là tâm đường tròn đi qua A,B, C
A
B