Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

= (x2-x+1)(x2+3x+10)+10 = P
x2-x+1=(x-\(\frac{1}{2}\))2+\(\frac{3}{4}\)>0
x2+3x+10=(x+\(\frac{3}{2}\))2+\(\frac{31}{4}\)>0
vây P>0



a) Ta có \(2x^2-8x+13=2x^2-8x+8+5\)
\(=2\left(x^2-4x+4\right)+5\)
\(=2\left(x-2\right)^2+5\ge5\forall x\)
Giả sử trước khi làm nhé
\(a)\)\(2x^2-8x+13>0\)
\(\Leftrightarrow\)\(4x^2-16x+26>0\)
\(\Leftrightarrow\)\(\left(4x^2-16+16\right)+10>0\)
\(\Leftrightarrow\)\(\left(2x-4\right)^2+10\ge10>0\) ( luôn đúng )
Vậy ...
\(b)\)\(-2+2x-x^2< 0\)
\(\Leftrightarrow\)\(x^2-2x+2>0\)
\(\Leftrightarrow\)\(\left(x^2-2x+1\right)+1>0\)
\(\Leftrightarrow\)\(\left(x-1\right)^2+1\ge1>0\) ( luôn đúng )
Vậy ...
Chúc bạn học tốt ~

a)2x(2x+7)=4(2x+7)
2x(2x+7)-4(2x+7)=0
(2x+7)(2x-4)=0
\(\Rightarrow\orbr{\begin{cases}2x+7=0\\2x-4=0\end{cases}}\)\(\Rightarrow\orbr{\begin{cases}x=-\frac{7}{2}\\x=2\end{cases}}\)
b)Ta có:x3-4x2+ax=x3-3x2-x2+ax
=x2(x-3)-x(x-a)
Để x3-4x2+ax chia hết cho x-3 thì a=3

a) kết quả là x^2-2x+3
b) CM NÈ:
X^2-2X+3=(X^2-2X+1)+2=(X-1)^2+2
VÌ (X-1)^2>=0 VỚI MỌI X=>(X-1)^2+2>0 VỚI MỌI x=> GIÁ TRỊ BIỂU THỨC LUÔN DƯƠNG

Biểu thức x + 1 x 2 xác định khi x ≠ 0
Biểu thức x 2 + 1 x 2 + 2 x + 1 1 x + 1 xác định khi x ≠ 0 và x ≠ - 1
Với điều kiện x ≠ 0 và x ≠ - 1, ta có:
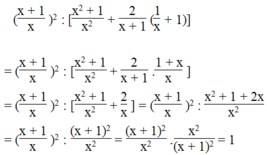
Vậy giá trị của biểu thức x + 1 x 2 : x 2 + 1 x 2 + 2 x + 1 1 x + 1 bằng 1 với mọi giá trị x ≠ 0 và x ≠ -1.
P = \(x^4-2x^3+2x^2-2x+1\)
P = \(x^4-x^3-x^3+x^2+x^2-x-x+1\)
P = \(x^3\left(x-1\right)-x^2\left(x-1\right)+x\left(x-1\right)-\left(x-1\right)\)
P = \(\left(x-1\right)\left(x^3-x^2+x-1\right)\)
P = \(\left(x-1\right)\left[x^2\left(x-1\right)+\left(x-1\right)\right]\)
P = \(\left(x-1\right)\left(x-1\right)\left(x^2+1\right)\)
P = \(\left(x-1\right)^2\left(x^2+1\right)\) \(\ge\forall x\) ( đpcm )
Chúc bạn học tốt :))