Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Theo giả thiết, nếu ba dố a, b, c lập thành cấp số nhân thì : \(ac=b^2\)(1)
Lấy Logarit cơ số N hai vế của (1) ta có :
\(\Leftrightarrow\log_N\left(ac\right)=\log_Nb^2\Leftrightarrow\log_Na+\log_Nc=2\log_Nb\left(2\right)\)
Sử dụng công thức đổi cơ số :
Từ (2) \(\Leftrightarrow\frac{1}{\log_aN}+\frac{1}{\log_cN}=\frac{2}{\log_bN}\Leftrightarrow\frac{1}{\log_aN}-\frac{1}{\log_bN}=\frac{1}{\log_bN}-\frac{1}{\log_cN}\)
\(\Leftrightarrow\frac{\log_bN-\log_aN}{\frac{1}{\log_aN}.\frac{1}{\log_bN}}=\frac{\log_cN-\log_bN}{\frac{1}{\log_cN}.\frac{1}{\log_bN}}\Leftrightarrow\frac{\log_bN-\log_aN}{\frac{1}{\log_cN}-\frac{1}{\log_bN}}=\frac{\log_aN}{\log_cN}\)
\(\Rightarrow\frac{\log_aN-\log_bN}{\frac{1}{\log_bcN}-\frac{1}{\log_cN}}=\frac{\log_aN}{\frac{1}{\log_cN}}\)
Ba số \(\frac{2}{{b - a}},\frac{1}{b},\frac{2}{{b - c}}\) theo thứ tự lập thành cấp số cộng nên ta có:
\(\begin{array}{l}\frac{2}{{b - a}} + \frac{2}{{b - c}} = 2.\frac{1}{b} \Leftrightarrow \frac{1}{{b - a}} + \frac{1}{{b - c}} = \frac{1}{b} \Leftrightarrow \frac{{\left( {b - c} \right) + \left( {b - a} \right)}}{{\left( {b - a} \right)\left( {b - c} \right)}} = \frac{1}{b}\\ \Leftrightarrow \frac{{b - c + b - {\rm{a}}}}{{{b^2} - ab - bc + ac}} = \frac{1}{b} \Leftrightarrow \frac{{2b - c - {\rm{a}}}}{{{b^2} - ab - bc + ac}} = \frac{1}{b} \Leftrightarrow b\left( {2b - c - {\rm{a}}} \right) = {b^2} - ab - bc + ac\\ \Leftrightarrow 2{b^2} - bc - {\rm{ab}} = {b^2} - ab - bc + ac \Leftrightarrow {b^2} = {\rm{a}}c\end{array}\).
Vậy ba số \(a,b,c\) theo thứ tự lập thành cấp số nhân.
Theo đầu bài ta có : \(\cot\frac{A}{2}+\cot\frac{C}{2}=2\cot\frac{B}{2}\Leftrightarrow\frac{\sin\frac{A+C}{2}}{\sin\frac{A}{2}\sin\frac{C}{2}}=2\frac{\cos\frac{B}{2}}{\sin\frac{B}{2}}=2\frac{\sin\frac{A+C}{2}}{\cos\frac{A+C}{2}}\)
\(\Leftrightarrow\sin\left(\frac{A+C}{2}\right)\cos\left(\frac{A+C}{2}\right)=2\sin\frac{A}{2}\sin\frac{C}{2}\sin\frac{A+C}{2}=\left(\cos\frac{A-C}{2}-\cos\frac{A+C}{2}\right)\sin\frac{A+C}{2}\)
\(\Leftrightarrow2\sin\frac{A+C}{2}\cos\frac{A+C}{2}=\cos\frac{A-C}{2}\sin\frac{A+C}{2}\)
\(\Leftrightarrow2\sin\left(A+C\right)=\frac{1}{2}\left(\sin A+\sin C\right)\)
\(\Leftrightarrow\sin A+\sin C=2\sin B\Rightarrow a+c=2b\)
Chứng tỏ 3 cạnh của tam giác lập thành cấp số cộng
Theo giả thiết ta có : \(\cot A+\cot C=2\cot B\)
\(\Leftrightarrow\frac{\sin\left(A+C\right)}{\sin A\sin C}=\frac{2\cos B}{\sin B}\)
\(\Leftrightarrow\sin^2B=2\sin B\sin C\cos B=\left[\cos\left(A-C\right)-\cos\left(A+C\right)\right]\cos B\)
\(\Leftrightarrow\sin^2B=\cos\left(A-C\right)\cos B-\cos\left(A+C\right)\cos B=-\cos\left(A-C\right)\cos\left(A+C\right)+\cos^2B\)
\(\Leftrightarrow\sin^2B=-\frac{1}{2}\left(\cos2A+\cos2C\right)+1-\sin^2B=-\frac{1}{2}\left(1-2\sin^2A+1-2\sin^2C\right)+1-\sin^2B\)
\(\Rightarrow2\sin^2B=\sin^2A+\sin^2C\Leftrightarrow2b^2=a^2+c^2\)
Vậy chứng tỏ \(a^2,b^2,c^2\) theo thứ tự đó cũng lập thành một cấp số cộng
Nếu 3 cạnh a, b, c lập thành cấp số cộng thì ta có a + c = 2b
\(\Leftrightarrow\sin A+\sin C=2\sin B\Leftrightarrow2\sin\frac{A+C}{2}\cos\frac{A-C}{2}=4\sin\frac{B}{2}\cos\frac{B}{2}\left(1\right)\)
Vì \(A+C=180^0-B\Rightarrow\frac{A+C}{2}=90^0-\frac{B}{2}\)
<=> \(\sin\frac{A+C}{2}=\sin\left(90^0-\frac{B}{2}\right)=\cos\frac{B}{2}\) hoặc \(\cos\frac{A+C}{2}=\cos\left(90^0-\frac{B}{2}\right)=\sin\frac{B}{2}\) (*)
Do đó (1) trở thành :
\(\Leftrightarrow\sin\frac{A+C}{2}\cos\frac{A-C}{2}=2\sin\frac{A+C}{2}\cos\frac{A+C}{2}\)
\(\Leftrightarrow\cos\frac{A-C}{2}=2\sin\frac{B}{2}\)
\(\Leftrightarrow\cos\frac{A-C}{2}=2\cos\frac{A+C}{2}\)
\(\Leftrightarrow\cos\frac{A}{2}\cos\frac{C}{2}+\sin\frac{A}{2}\sin\frac{C}{2}=2\cos\frac{A}{2}\cos\frac{C}{2}-2\sin\frac{A}{2}\sin\frac{C}{2}\)
\(\Leftrightarrow\cos\frac{A}{2}\cos\frac{C}{2}=3\sin\frac{A}{2}\sin\frac{C}{2}\)
\(\Leftrightarrow\cot\frac{A}{2}\cot\frac{C}{2}=3\) => Điều phải chứng minh
gọi a,b,c là 3 cạnh của tam giác.
Ta có :\(cot\left(\dfrac{A}{2}\right)+cot\left(\dfrac{C}{2}\right)=2cot\left(\dfrac{B}{2}\right)\) <=> \(\dfrac{cot\left(\dfrac{A}{2}\right)}{sin\left(\dfrac{A}{2}\right)}+\dfrac{cos\left(\dfrac{C}{2}\right)}{sin\left(\dfrac{C}{2}\right)}=\dfrac{2.cos\left(\dfrac{B}{2}\right)}{sin\left(\dfrac{B}{2}\right)}\)
<=> \(\dfrac{sin\left(\dfrac{C}{2}\right)cos\left(\dfrac{A}{2}\right)+cos\left(\dfrac{C}{2}\right)sin\left(\dfrac{A}{2}\right)}{sin\left(\dfrac{A}{2}\right).sin\left(\dfrac{C}{2}\right)}=2.\dfrac{cos\left(\dfrac{B}{2}\right)}{sin\left(\dfrac{C}{2}\right)}\)
<=> \(\dfrac{sin\left(\dfrac{A}{2}+\dfrac{C}{2}\right)}{sin\left(\dfrac{A}{2}\right)sin\left(\dfrac{C}{2}\right)}=2.\dfrac{cos\left(\dfrac{B}{2}\right)}{sin\left(\dfrac{B}{2}\right)}\) <=> \(\dfrac{cos\left(\dfrac{B}{2}\right)}{sin\left(\dfrac{A}{2}\right)sin\left(\dfrac{C}{2}\right)}=2.\dfrac{cos\left(\dfrac{B}{2}\right)}{sin\left(\dfrac{B}{2}\right)}\)
<=> \(sin\left(\dfrac{B}{2}\right).cos\left(\dfrac{B}{2}\right)=2sin\left(\dfrac{A}{2}\right)sin\left(\dfrac{C}{2}\right)cos\left(\dfrac{B}{2}\right)\)
<=> \(\dfrac{1}{2}sinB=\left[cos\left(\dfrac{A}{2}-\dfrac{C}{2}\right)-cos\left(\dfrac{A}{2}+\dfrac{C}{2}\right)\right]cos\left(\dfrac{B}{2}\right)\)
<=>\(\dfrac{1}{2}sinB=cos\left(\dfrac{A}{2}-\dfrac{C}{2}\right).cos\left(\dfrac{B}{2}\right)-sin\left(\dfrac{B}{2}\right)cos\left(\dfrac{B}{2}\right)\)
<=> \(\dfrac{1}{2}sinB=cos\left(\dfrac{A}{2}-\dfrac{C}{2}\right)sin\left(\dfrac{A}{2}+\dfrac{C}{2}\right)-\dfrac{1}{2}sinB\)
<=> sinB = \(\dfrac{1}{2}\left(sinA+sinC\right)\) <=> \(2sinB=sinA+sinC\)
<=> \(2.\dfrac{b}{2R}=\dfrac{a}{2R}+\dfrac{c}{2R}\)
<=> a+c =2b
=> 3 cạnh của tam giác tạo thành cấp số cộng.
Chọn A.
Phương pháp:
Ba số x, y, z lập thành một cấp số cộng
⇔ x + z - 2 y
Và số x, y, z lập thành một cấp số nhân ⇔ x z = y 2
Cách giải
Do 3 số x, y, z lập thành một cấp số cộng và có tổng bằng 21 nên ta có
x + z = 2 y x + y + z = 21
⇔ x + z = 14 y = 7
⇔ x = 14 - z y = 7 ( 1 )
Nếu lần lượt thêm các số 2; 3; 9 vào ba số đó (theo thứ tự của cấp số cộng)
thì được ba số lập thành một cấp số nhân nên ta có
( x + 2 ) ( z + 9 ) = ( y + 3 ) 2 ( 2 )
Thay (1) vào (2) ta có:
( 14 - z + 2 ) ( z + 9 ) = ( 7 + 3 ) 2
⇔ z 2 - 7 z - 44 = 0
⇔ z = 11 z = - 4
z = 11 ⇒ z = 14 - 11 = 3
⇒ F = x 2 + y 2 + z 2 = 179
z = - 4 ⇒ x = 14 - ( - 4 ) = 18
⇒ F = x 2 + y 2 + z 2 = 389
Chọn C
*Theo tính chất của cấp số cộng , ta có x+ z = 2y.
Kết hợp với giả thiết, x+ y + z = 21, ta suy ra 3y = 21 nên y = 7.
* Gọi d là công sai của cấp số cộng thì x = y − d = 7 − d và z = y + d = 7 + d .
Sau khi thêm các số 2 ; 3 ; 9 vào ba số x ; y ; z ta được ba số là x+ 2 ; y + 3 ; z + 9 hay
9- d ; 10 ; 16+ d.
* Theo tính chất của cấp số nhân, ta có
9 − d 16 + d = 10 2 ⇔ d 2 + 7 d − 44 = 0
Giải phương trình ta được d= -11 hoặc d= 4.
Với d = -11 ; cấp số cộng 18 ; 7 ; - 4. Lúc này F = 389.
Với d= 4, cấp số cộng 3 ; 7 ; 11. Lúc này F = 179.
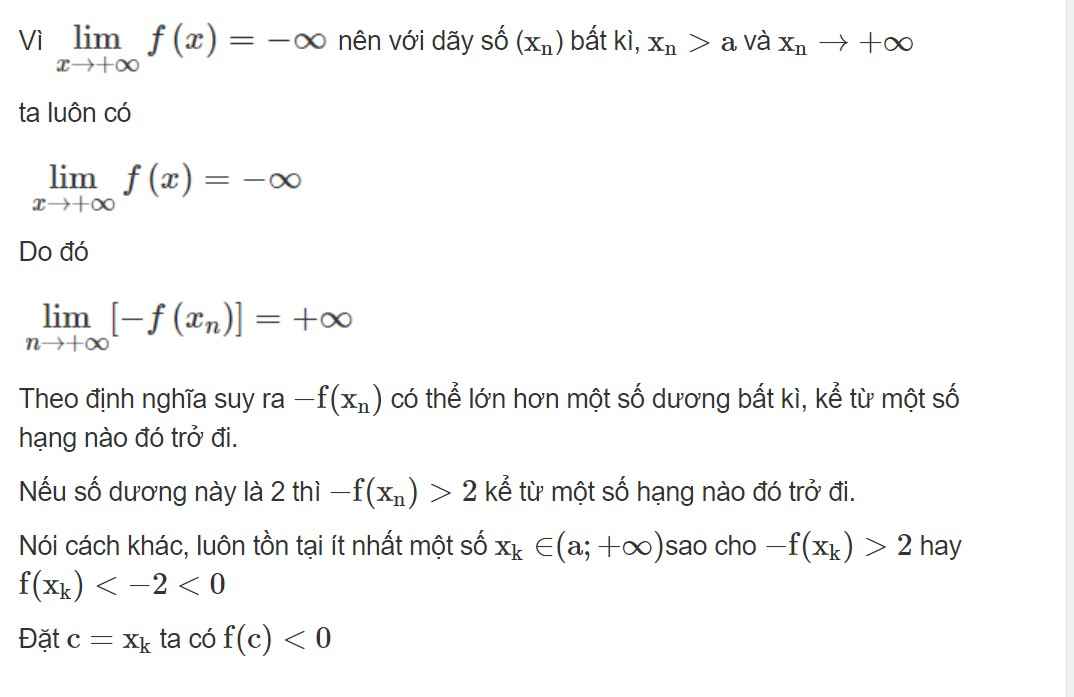
Theo giả thiết :
\(\Leftrightarrow\log_xa+\log_zc=2\log_yb\)
\(\Leftrightarrow\frac{1}{\log_ax}+\frac{1}{\log_cz}=\frac{2}{\log_by}\)
\(\Rightarrow\frac{1}{\log y_b}=\frac{2\log_ax.\log_cz}{\log_ax+\log_cz}\)
\(\Rightarrow\) Điều phải chứng minh