Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì Ox // O'x' nên \(\widehat{O_1}=\widehat{O'_1}\) (2 góc đồng vị) (1)
Vì Oy // O'y' nên \(\widehat{O_2}=\widehat{O'_2}\) (2 góc đồng vị) (2)
Từ (1) và (2) suy ra:
\(\widehat{O_1}-\widehat{O_2}=\widehat{O'_1}-\widehat{O'_2}\)
hay \(\widehat{xOy}=\widehat{x'O'y'}\).

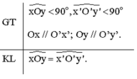
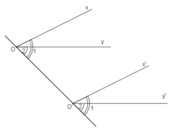
Chứng minh:
Vẽ đường thẳng OO’
Vì Ox // O’x’ nên hai góc đồng vị ∠(O1) và ∠(O'1) bằng nhau
Suy ra: ∠(O1) = ∠(O'1 ) (1)
Vì Oy // O’y’ nên hai góc đồng vị ∠(O2) và ∠(O'2) bằng nhau
Suy ra: ∠(O2) = ∠(O'2)(2)
Từ (1) và (2) suy ra: ∠(O1) - ∠(O2) =∠(O'1) - ∠(O'2)
Vậy ∠(xOy) = ∠(x'O'y')

Đặt H là giao điểm của Oy và O'x'
Vì Ox//O'x'
=>O1ˆO1^=H1ˆH1^( đồng vị)
Vì Oy//O'y'
=>H1ˆH1^=O′1ˆO1′^( đồng vị)
Do đó:O1ˆO1^=O′1ˆO1′^
VậyxOyˆ=x′O′y′ˆxOy^=x′O′y′^
x x* y y* o o* 1 1 h1

bài này mk làm rồi nhưng quên rồi