

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



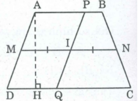
Giả sử hình thang ABCD có AB // CD, đường trung bình là MN. Gọi I là trung điểm của MN, đường thẳng bất kỳ đi qua I cắt AB tại P và CD tại Q.
Ta có hai hình thang APQD và BPQC có cùng đường cao.
MI là đường trung bình của hình thang APQD.
Suy ra: MI = 1/2 (AP + QD)
IN là đường trung bình của hình thang BPQC.
Suy ra: IN = 1/2 (BP + QC)
S A P Q D = 1/2 (AP + QD).AH = MI.AH (1)
S B P Q C = 1/2 (BP + QC).AH = IN.AH (2).
IM = IN (gt) (3)
Từ (1), (2) và (3) suy ra: S A P Q D = S B P Q C , các giá trị này không phụ thuộc vào vị trí của P và Q.

A B C D E M h N
Kéo dài AB về phía B một đoạn BE=DC. Nối DE cắt BC tại M.
Do CD // BE nên ta có tam giác MDC = tam giác MEB (trường hợp g.c.g). Suy ra dt(ABCD)=dt(ABMD) + dt(MDC) = dt(ABMD) + dt(MEB) = dt(DAE) = 1/2 .AE . h =1/2 (AB + BE).h = \(\dfrac{AB+CD}{2}.h\)
b) Theo câu a) thì diện tích hình thang ABCD bằng diện tích tam giác DAE nên ta nối D với trung điểm N của AE thì DN sẽ chia tam giác DAE thành 2 phần bằng nhau. Khi đó diện tích tam giác DAN bằng nửa diện tích hình thang ABCD.

Câu hỏi của Lưu Đức Mạnh - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo bài giải tại đây nhé.

1.
O A B D C E
+) Tứ giác ABCD kà hình thang cân => góc ADC = BCD và AD = BC
=> tam giác ODC cân tại O => OD = OC
mà AD = BC => OA = OB
+) tam giác ODB và OCA có: OD = OC; góc DOC chung ; OB = OA
=> Tam giác ODB = OCA (c - g - c)
=> góc ODB = OCA mà góc ODC = OCD => góc ODC - ODB = OCD - OCA
=> góc EDC = ECD => tam giác EDC cân tại E => ED = EC (2)
Từ (1)(2) => OE là đường trung trực của CD
=> OE vuông góc CD mà CD // AB => OE vuông góc với AB
Tam giác OAB cân tại O có OE là đường cao nên đồng thời là đường trung trực
vậy OE là đường trung trực của AB