Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử A = {a, b} với a, b là hai số tự nhiên khác nhau từ 1 đến 15.
Ta có \(\left(1+2+...+15\right)-\left(a+b\right)=ab\)
\(\Leftrightarrow\left(a+1\right)\left(b+1\right)=121\).
Do a, b > 0 nên a = b = 10 (vô lí).
Vậy....

Giải thích các bước giải:
Giả sử chúng ta chia được một tập `S=n,n+1,…n+17` của `18` số nguyên dương liên tiếp thành tập `A, B` sao cho ∏n∈Aa=∏n∈Bb và tách của các phần tử trong A bằng tích của các phần tử trong B, nếu 1 tập chứa bội số của 19 thì tập còn lại cũng như thế.
Do vậy, S không chứa bội số nào của 19 hoặc chứa ít nhất hai bội số của 19. Vì có duy nhất 1 trong 18 số nguyên dương liên tiếp có thể là bội của 19, S phải không chứa bội số nào. Bởi vậy `n,n+1,…n+17` lần lượt đồng dư `1,2,3,…,18\ mod\ 19` (chia lấy dư). Do vậy, theo quy tắc Wilson:
∏n∈Aa×∏n∈Bb=n(n+1)+…(n+17)=18!=−1 (mod 19)
Tuy nhiên hai tích của bên trái bằng nhau, điều này không có khả năng vì `-1` không là bình phương của phép mod 19. Bởi vậy, không tồn tại hai tập A và B
Hok tốt!!!!!!!!

Đáp án C
Ta tìm số cặp số (a;b) thoả mãn
![]()
![]()
Có 49 cặp (a;b) thỏa mãn. Do đó S gồm 49 phần tử:
Ta tìm số cặp (a;b) thoả mãn
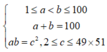
![]()
Do đó 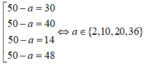
Vậy có 4 cặp số (a;b)có tổng bằng 100 và tích của chúng là một số chính phương.

Chọn D
Gọi số tự nhiên có chữ số khác nhau lấy từ các phần tử của tập A là ![]()
![]()
+) Chọn a có 6 cách.
+) Chọn bốn chữ số b,c,d,e có A 6 4 cách.
Vậy số cách lập số tự nhiên có 5 chữ số khác nhau lấy từ các phần tử của tập A là
6.
A
6
4
= 2160 cách. Do đó số phần tử của không gian mẫu là ![]()
Gọi biến cố B: ‘‘Số tự nhiên lập được chia hết cho 5 và các chữ số 1,2,3 luôn có mặt cạnh nhau’’.
TH1: Số lập được có dạng a b c d 0 ¯
+) Vì các chữ số 1,2,3 luôn có mặt cạnh nhau nên ta coi ba số đó là khối X. Xếp ba số 1,2,3 trong khối X có P 3 cách.
+) Chọn 1 số trong tập ![]()
+) Xếp khối X và số vừa chọn vào vị trí có P 2 cách.
Theo quy tắc nhân ta có P 3 .3 P 2 = 36 số.
TH2: Số lập được có dạng a b c 05 ¯
+) Vì các chữ số 1,2,3 luôn có mặt cạnh nhau nên ta có P 3 cách chọn số a,b,c
Vậy có P 3 = 6 số.
TH3: Số lập được có dạng ![]()
+) Vì các chữ số 1,2,3 luôn có mặt cạnh nhau nên ta coi ba số đó là khối X. Xếp ba số 1,2,3 trong khối X có P 3 cách.
+) Chọn số trong tập {4;6} có C 2 1 = 2 cách.
+) Xếp khối X và số vừa chọn vào vị trí có P 2 cách.
Theo quy tắc nhân ta có P 3 .2 P 2 = 24 số.
Vậy số kết quả xảy ra của biến cố B là ![]()
Xác suất của biến cố B là 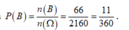

#include <bits/stdc++.h>
using namespace std;
int B[100],n,t;
{
cin>>n;
for (int i=1; i<=n; i++) cin>>B[i];
t=0;
for (int i=1; i<=n; i++)
if (B[i]%10==0) t+=B[i];
cout<<t<<endl;
int dem=0;
for (int i=1; i<=n; i++)
if ((i%2==0) && (A[i]%2!=0)) dem++;
cout<<dem<<endl;
for (int i=1; i<=n; i++)
if ((A[i]%2!=0) && (A[i]%3==0)) cout<<A[i];
}
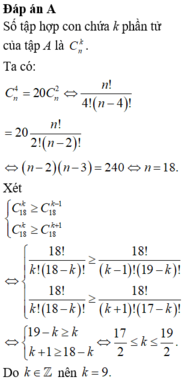
xin lỗi nha mình chịu