Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có :
<=> u3 - 3u - 2 \(\le\) v3 - 3v + 2 <=> ( u + 1 )2( u - 2 ) \(\le\) ( v - 1 )2( v + 2 )
Đặt x = u + 1 , y = v -1 thì :
BĐT <=> x3 - 3x2 \(\le\) y3 + 3y2 <=> x3 - y3 \(\le\) 3(x2 + y2)
Ta có : x - y = ( u - v ) + 2 \(\le\)2
=> ( x - y ) ( x2 + xy + y2 ) \(\le\)2( x2 + xy + y2) = 2(x2 + y2) + 2xy \(\le\) 2(x2 + y2) + ( x2 + y2 ) = 3(x2 + y2 ) => x3 - y3 \(\le\) 3(x2 +y2 ) ( đpcm)
Dấu bằng xảy ra khi <=> x = y = 0 <=> u = -1 ; v = 1
\(cotx-tanx=\frac{cosx}{sinx}-\frac{sinx}{cosx}=\frac{cos^2x-sin^2x}{sinx.cosx}=\frac{cos2x}{\frac{1}{2}sin2x}=2cot2x\)
\(\frac{cos^2x-sin^2x}{1+sin2x}=\frac{\left(cosx-sinx\right)\left(cosx+sinx\right)}{sin^2x+cos^2x+2sinx.cosx}=\frac{\left(cosx-sinx\right)\left(cosx+sinx\right)}{\left(cosx+sinx\right)^2}=\frac{cosx-sinx}{cosx+sinx}\)
\(=\frac{\frac{cosx}{cosx}-\frac{sinx}{cosx}}{\frac{cosx}{cosx}+\frac{sinx}{cosx}}=\frac{1-tanx}{1+tanx}\)
Nhân cả tử và mẫu vế trái với \(cos2x.cosx\) ta được:
\(\frac{sin2x.sinx}{sin2x.cosx-cos2x.sinx}=\frac{sin2x.sinx}{sin\left(2x-x\right)}=\frac{sin2x.sinx}{sinx}=sin2x\)
\(cotx-tanx-2tan2x=\frac{cosx}{sinx}-\frac{sinx}{cosx}-\frac{2sin2x}{cos2x}\)
\(=\frac{cos^2x-sin^2x}{\frac{1}{2}.2.sinxcosx}=\frac{cos2x}{\frac{1}{2}sin2x}=2\left(\frac{cos2x}{sin2x}-\frac{sin2x}{cos2x}\right)\)
\(=2\left(\frac{cos^22x-sin^22x}{\frac{1}{2}2sin2xcos2x}\right)=4\frac{cos4x}{sin4x}=4cot4x\)
\(\frac{2}{sin4x}-tan2x=\frac{2}{2sin2x.cos2x}-\frac{sin2x}{cos2x}=\frac{1}{cos2x}\left(\frac{1}{sin2x}-sin2x\right)\)
\(=\frac{1}{cos2x}\left(\frac{1-sin^22x}{sin2x}\right)=\frac{1}{cos2x}\frac{cos^22x}{sin2x}=\frac{cos2x}{sin2x}=cot2x\)
\(\frac{sin2x}{1+cos2x}=\frac{2sinxcosx}{1+2cos^2x-1}=\frac{2sinxcosx}{2cos^2x}\)
\(=\frac{sinx}{cosx}=tanx\)
Đề bài sai, kết quả ra tan chứ ko phải cot
Ta chứng minh hai mệnh đề.
a) Cho
= 
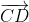thì AD và BC có trung điểm trùng nhau. Gọi I là trung điểm của AD ta chứng minh I cũng là trung điểm của BC.
Theo quy tắc của ba điểm của tổng, ta có
= 
+ 
;
Vì
= 
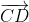nên 
+ 
= 
+ 
=>
– 
= 
– 
=>
+ 
= 
+ 
(1)
Vì I là trung điểm của AD nên
+ 
= 
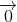(2)
Từ (1) và (2) suy ra
+ 
= 
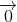(3)
Đẳng thức (3) chứng tỏ I là trung điểm của BC.
b) AD và BC có chung trung điểm I, ta chứng minh
= 
.
I là trung điểm của AD =>
+ 
= 
=> 
– 
=
I là trung điểm của BC =>
+ 
= 
=> 
– 
= 
Suy ra
– 
= 
– 
=>
+ 
= 
+ 
=> 
= 
(đpcm)