Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có: \(C=\dfrac{1}{101}+\dfrac{1}{102}+\dfrac{1}{103}+...+\dfrac{1}{200}\)
\(=\left(\dfrac{1}{101}+\dfrac{1}{102}+...+\dfrac{1}{120}\right)+\left(\dfrac{1}{121}+\dfrac{1}{122}+\dfrac{1}{123}+...+\dfrac{1}{150}\right)+\left(\dfrac{1}{151}+\dfrac{1}{152}+\dfrac{1}{153}+...+\dfrac{1}{180}\right)+\left(\dfrac{1}{181}+\dfrac{1}{182}+\dfrac{1}{183}+...+\dfrac{1}{200}\right)\)
\(\Leftrightarrow C>20\cdot\dfrac{1}{120}+30\cdot\dfrac{1}{150}+30\cdot\dfrac{1}{180}+20\cdot\dfrac{1}{200}\)
\(\Leftrightarrow C>\dfrac{1}{6}+\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{10}=\dfrac{19}{30}=\dfrac{76}{120}\)
\(\Leftrightarrow C>\dfrac{75}{120}=\dfrac{5}{8}\)
hay \(C>\dfrac{5}{8}\)(đpcm)
a: A>1/150*50+1/200*50=1/3+1/4=7/12
b: A>7/12
7/12>5/8
=>A>5/8
c) P = \(\dfrac{1}{101}+\dfrac{1}{102}+\dfrac{1}{103}+...+\dfrac{1}{200}\)
\(=\left(\dfrac{1}{101}+\dfrac{1}{102}+...+\dfrac{1}{150}\right)+\left(\dfrac{1}{151}+\dfrac{1}{152}+...+\dfrac{1}{200}\right)\)
Dễ thấy \(\dfrac{1}{101}+\dfrac{1}{102}+...+\dfrac{1}{150}>\dfrac{1}{150}+\dfrac{1}{150}+...+\dfrac{1}{150}\)(50 hạng tử)
\(\Leftrightarrow\dfrac{1}{101}+\dfrac{1}{102}+...+\dfrac{1}{150}>\dfrac{1}{150}.50=\dfrac{1}{3}\)(1)
Tương tự
\(\dfrac{1}{151}+\dfrac{1}{152}+...+\dfrac{1}{200}>\dfrac{1}{200}+\dfrac{1}{200}+...+\dfrac{1}{200}\)(50 hạng tử)
\(\Leftrightarrow\dfrac{1}{151}+\dfrac{1}{152}+...+\dfrac{1}{200}>50.\dfrac{1}{200}=\dfrac{1}{4}\)(2)
Từ (1) và (2) ta được
\(P>\dfrac{1}{3}+\dfrac{1}{4}=\dfrac{7}{12}\)
P = \(\dfrac{1}{101}+\dfrac{1}{102}+\dfrac{1}{103}+...+\dfrac{1}{200}\)
\(=\left(\dfrac{1}{101}+\dfrac{1}{102}+...+\dfrac{1}{150}\right)+\left(\dfrac{1}{151}+\dfrac{1}{152}+...+\dfrac{1}{200}\right)\)
\(\overline{50\text{ hạng tử }}\) \(\overline{50\text{ hạng tử }}\)
\(< \left(\dfrac{1}{100}+\dfrac{1}{100}+...+\dfrac{1}{100}\right)+\left(\dfrac{1}{150}+\dfrac{1}{150}+...+\dfrac{1}{150}\right)\)
\(=\dfrac{1}{100}.50+\dfrac{1}{150}.50=\dfrac{1}{2}+\dfrac{1}{3}=\dfrac{5}{6}\)
\(\Rightarrow P< \dfrac{5}{6}< 1\)
Ta có:
\(\dfrac{1}{101}>\dfrac{1}{150}\)
\(\dfrac{1}{102}>\dfrac{1}{150}\)
....
\(\dfrac{1}{150}=\dfrac{1}{150}\)
=>\(\dfrac{1}{101}+\dfrac{1}{102}+...+\dfrac{1}{150}>\dfrac{1}{150}+\dfrac{1}{150}+...+\dfrac{1}{150}\)(50 số)=\(\dfrac{1}{3}\)
Ta có:
\(\dfrac{1}{152}>\dfrac{1}{200}\)
\(\dfrac{1}{153}>\dfrac{1}{200}\)
....
\(\dfrac{1}{200}=\dfrac{1}{200}\)
=>\(\dfrac{1}{151}+\dfrac{1}{153}+...+\dfrac{1}{120}>\dfrac{1}{120}+\dfrac{1}{120}+...+\dfrac{1}{120}\)(50 số)=\(\dfrac{1}{4}\)
=>\(\dfrac{1}{101}+\dfrac{1}{102}+...+\dfrac{1}{200}>\dfrac{1}{3}+\dfrac{1}{4}\)
=> \(A>\dfrac{7}{12}\)
\(B=\left(\dfrac{1}{101}+\dfrac{1}{102}+...+\dfrac{1}{150}\right)+\left(\dfrac{1}{151}+...\dfrac{1}{200}\right)>\dfrac{1}{150}+..\dfrac{1}{150}+\dfrac{1}{200}+..+200=\dfrac{50}{150}+\dfrac{50}{200}=\dfrac{1}{3}+\dfrac{1}{4}=\dfrac{4}{12}+\dfrac{3}{12}=\dfrac{7}{12}\)Vậy ... (ta có điều phải chứng minh )
Ta có :\(\dfrac{1}{20}>\dfrac{1}{200}\)
...
\(\dfrac{1}{199}>\dfrac{1}{200}\)
Do đó : \(\dfrac{1}{20}+\dfrac{1}{21}+...+\dfrac{1}{200}>\dfrac{1}{200}+\dfrac{1}{200}+..+\dfrac{1}{200}=\dfrac{181}{200}>\dfrac{180}{200}=\dfrac{9}{10}\)Vậy ...
Ta có: \(\dfrac{1}{101}>\dfrac{1}{200}\)
Tương tự ta có: \(\dfrac{1}{102}>\dfrac{1}{200}\) ;....; \(\dfrac{1}{199}>\dfrac{1}{200}\)
\(\Rightarrow\dfrac{1}{101}+\dfrac{1}{102}+\dfrac{1}{103}+...+\dfrac{1}{199}+\dfrac{1}{200}>\dfrac{1}{200}.100\)
\(\Leftrightarrow\dfrac{1}{101}+\dfrac{1}{102}+\dfrac{1}{103}+...+\dfrac{1}{199}+\dfrac{1}{200}>\dfrac{100}{200}\)
\(\Leftrightarrow\dfrac{1}{101}+\dfrac{1}{102}+\dfrac{1}{103}+...+\dfrac{1}{199}+\dfrac{1}{200}>\dfrac{1}{2}\left(đpcm\right)\)
\(1-\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{199}-\dfrac{1}{200}\)
\(=\left(1+\dfrac{1}{3}+...+\dfrac{1}{199}\right)-\left(\dfrac{1}{2}+\dfrac{1}{4}+..+\dfrac{1}{200}\right)\)
\(=\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{199}+\dfrac{1}{200}\right)-2\left(\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{200}\right)\)
\(=\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{199}+\dfrac{1}{200}\right)-\left(1+\dfrac{1}{2}+...+\dfrac{1}{100}\right)\)
\(=\dfrac{1}{101}+...+\dfrac{1}{199}+\dfrac{1}{200}\)
refer
https://hoc247.net/hoi-dap/toan-6/chung-minh-1-101-1-102-1-103-1-104-1-299-1-300-2-3-faq302038.html
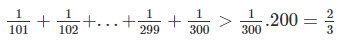
Ta có:
\(\dfrac{1}{101}+\dfrac{1}{102}+\dfrac{1}{103}+...+\dfrac{1}{150}>\dfrac{1}{150}+\dfrac{1}{150}+\dfrac{1}{150}+\dfrac{1}{150}+...+\dfrac{1}{150}\) (có 50 số hạng)
⇔ \(\dfrac{1}{101}+\dfrac{1}{102}+\dfrac{1}{103}+...+\dfrac{1}{150}>\dfrac{1}{3}\) \(\left(1\right)\)
\(\dfrac{1}{151}+\dfrac{1}{152}+\dfrac{1}{153}+...+\dfrac{1}{200}>\dfrac{1}{200}+\dfrac{1}{200}+\dfrac{1}{200}+...+\dfrac{1}{200}\) (có 50 số hạng)
⇔ \(\dfrac{1}{151}+\dfrac{1}{152}+\dfrac{1}{153}+...+\dfrac{1}{200}>\dfrac{1}{4}\) \(\left(2\right)\)
Từ (1) và (2), cộng vế theo vế. Ta được:
\(\dfrac{1}{101}+\dfrac{1}{102}+\dfrac{1}{103}+...+\dfrac{1}{150}+\dfrac{1}{151}+\dfrac{1}{152}+\dfrac{1}{153}+...+\dfrac{1}{200}>\dfrac{1}{3}+\dfrac{1}{4}=\dfrac{7}{12}\)
⇒ \(ĐPCM\)
Cậu nghĩ đâu mà hay vậy