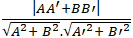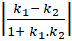Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử có 2 đường thẳng a và a’ đi qua A và vuông góc với d.
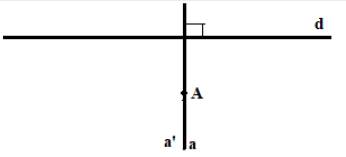
Vì a \( \bot \) d, mà a’ \( \bot \) d nên a // a’ (hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau)
Mà A \( \in \) a, A \( \in \) a'
\( \Rightarrow a \equiv a'\)
Vậy có duy nhất đường thẳng đi qua A và vuông góc với d.

Trả lười :
Câu 6: Cho trước một điểm A và một đường thẳng d có ...........1 và chỉ 1............... đường thẳng d’đi qua A và vuông góc với d.
~~Học tốt~~
Cho đường thẳng ∆ và điểm M(a; b). Viết phương trình đường thẳng d đi qua M và tạo với đường thẳng ∆ một góc α.
+ Cách 1:
- Gọi n→(A; B) là VTPT của đường thẳng d.
Tìm VTPT n'→( A’; B’) của đường thẳng ∆.
- Do góc giữa đường thẳng d và ∆ bằng α nên:
Cosα =
Giải phương trình trên ta được A = k.B. Chọn A =.... ⇒ B..
⇒ VTPT của đường thẳng d
⇒ Phương trình đường thẳng d.
+ Cách 2:
- Đường thẳng ∆ có hệ số góc k1.
- Giả sử đường thẳng d có hệ số góc k2.
- Do góc giữa hai đường thẳng d và ∆ là α nên :
Tanα =
Phương trình trên là phương trình ẩn k2. Giải hệ phương trình ta được k2
⇒ Phương trình đường thẳng d.