K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
18 tháng 10 2019
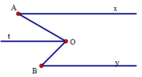
Qua O kẻ d sao cho d / / A x / / B y .
O 1 ^ = 50 ° = y B O ^ ( so le trong); O 2 ^ = O A x ^ = 40 ° ( so le trong)
⇒ O ^ = 40 ° + 50 ° = 90 °
PT
1
CM
25 tháng 3 2017
Qua điểm O kẻ tia Ot // Ox. Khi đó,
A
^
=
A
O
x
^
(2 góc so le trong).
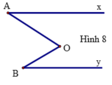
Do O t ∥ O x O y ∥ O x nên O t ∥ O y , B ^ = B O t ^ (2 góc so le trong)
Từ đó, ta có A O B ^ = A O t ^ + t O B ^ = A ^ + B ^ .
Vậy A ^ + B ^ = A O B ^ (đpcm)
KV
30 tháng 8 2023
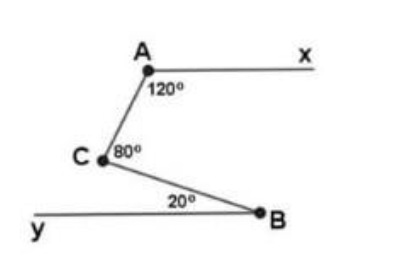
a) Vẽ tia By' là tia đối của tia By
Ta có:
∠ABy' + ∠ABy = 180⁰ (kề bù)
⇒ ∠ABy' = 180⁰ - ∠ABy
= 180⁰ - 135⁰
= 45⁰
⇒ ∠ABy' = ∠BAx = 45⁰
Mà ∠ABy' và ∠BAx là hai góc so le trong
⇒ By // Ax
b) Ta có:
∠CBy' = ∠ABC - ∠ABy'
= 75⁰ - 45⁰
= 30⁰
⇒ ∠CBy' = ∠BCz = 30⁰
Mà ∠CBy' và ∠BCz là hai góc so le trong
⇒ By // Cz
HN
1
29 tháng 6 2017
ta có :
A,B,C tỉ lệ với a,b,c
\(\Rightarrow\frac{A}{a}=\frac{B}{b}=\frac{C}{c}\)
đặt \(\frac{A}{a}=\frac{B}{b}=\frac{C}{c}=k\)
\(\Rightarrow\)A = ak ; B = bk ; C = ck
\(\Rightarrow Q=\frac{akx+bky+ck}{ax+by+c}=\frac{k.\left(ax+by+c\right)}{ax+by+c}=k\)
Vậy giá trị của Q không phụ thuộc vào x và y
G
21 tháng 12 2017
Ta có: \(x+y+z=\left(by+cz\right)+\left(ax+cz\right)+\left(ax+by\right)=2\left(ax+by+cz\right)\)
=> \(x+y+z=2\left(ax+by+cz\right)=2\left[\left(ax+by\right)+cz\right]=2\left[z+cz\right]=2\left(1+c\right)z\)
=> \(\frac{1}{1+c}=\frac{2z}{x+y+z}\) (1)
Tượng tự:
\(\frac{1}{1+a}=\frac{2x}{x+y+z}\) (2)
\(\frac{1}{1+b}=\frac{2y}{x+y+z}\) (3)
Cộng các vế của (1), (2), (3) ta có:
\(\frac{1}{1+a}+\frac{1}{1+b}+\frac{1}{1+c}=\frac{2\left(x+y+z\right)}{x+y+z}=2\) (ĐPCM)
10 tháng 5 2020
Ta có x+y=ax+by+2cz=z+2cz
=> x+y-z=2cz
=> \(c=\frac{x+y-z}{2z}\Rightarrow c+1=\frac{x+y-z}{2z}+1=\frac{x+y+z}{2z}\)
\(\Rightarrow\frac{1}{c+1}=\frac{2z}{x+y+z}\left(1\right)\)
\(y+z=2ax+by+cz\Rightarrow y+z-x=2ax\Rightarrow a=\frac{y+z-x}{2x}\Rightarrow a+1=\frac{x+y+z}{2x}\)
\(\Rightarrow\frac{1}{a+1}=\frac{2x}{x+y+z}\left(2\right)\)
\(z+x=2by+ax+cz=2by+y\Rightarrow z+x-y=2by\)
\(\Rightarrow b=\frac{z+x-y}{2y}\Rightarrow b+1=\frac{z+x-y}{2y}+1=\frac{x+y+z}{2y}\)
\(\Rightarrow\frac{1}{b+1}=\frac{2y}{x+y+z}\left(3\right)\)
Cộng từng vế của (1)(2)(3) ta có
\(\frac{1}{a+1}+\frac{1}{b+1}+\frac{1}{c+1}=\frac{2x}{x+y+z}+\frac{2y}{x+y+z}+\frac{2z}{x+y+z}=\frac{2\left(x+y+z\right)}{x+y+z}=2\)
a) ch
4 tháng 8 2023
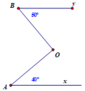
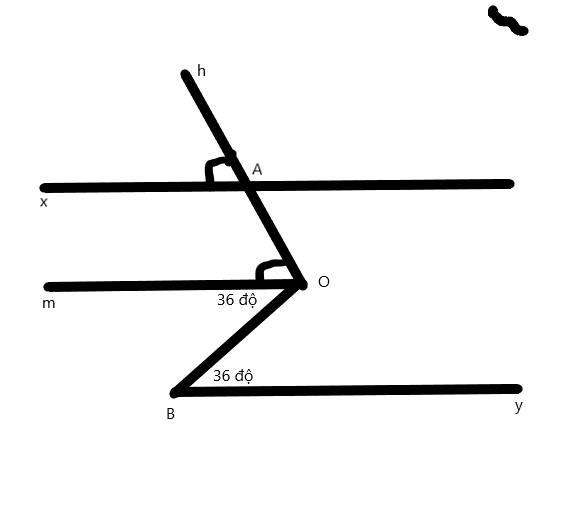
a: góc hAx=góc mOA
mà hai góc này đồng vị
nên Ax//Om
b: góc mOA=góc yBO
mà hai góc này so le trong
nên Om//By
mà Ax//Om
nên Ax//By
H9
HT.Phong (9A5)
CTVHS
4 tháng 8 2023
a) Ta có:
\(\widehat{xAh}=\widehat{mOA}\) (gt) nên hai góc này là hai góc đồng vị
⇒ Ax//Om
b) Ta có:
\(\widehat{OBy}=\widehat{mOB}=36^o\) nên hai góc này là hai góc so le trong
⇒ By//Om
Mà: Ax//Om (cmt)
⇒ Ax//By
Ax//By khi mà nó // với nhau
???? tự nhiên chứng minh ax //by