NT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 4 2020
a/ \(\left\{{}\begin{matrix}\left(SAB\right)\perp\left(ABCD\right)\\\left(SAD\right)\perp\left(ABCD\right)\\\left(SAB\right)\cap\left(SAD\right)=SA\end{matrix}\right.\) \(\Rightarrow SA\perp\left(ABCD\right)\)
b/ \(SA\perp\left(ABCD\right)\Rightarrow AB\) là hình chiếu vuông góc của SB lên (ABCD)
\(\Rightarrow\widehat{SBA}\) là góc giữa SB và (ABCD)
\(tan\widehat{SBA}=\frac{SA}{AB}=2\Rightarrow\widehat{SBA}\approx63^026'\)
c/ \(AB=BC\Rightarrow\Delta ABC\) cân tại B
\(\Rightarrow\) BO là trung tuyến đồng thời là đường cao
\(\Rightarrow BO\perp AC\)
Mà \(SA\perp\left(ABCD\right)\Rightarrow SA\perp BO\)
\(\Rightarrow BO\perp\left(SAC\right)\Rightarrow\left(SBO\right)\perp\left(SAC\right)\)
d/ \(AC=AB\sqrt{2}=a\sqrt{2}\)
Gọi M là trung điểm AD \(\Rightarrow AM=\frac{AD}{2}=a\Rightarrow CM=MD=a\)
\(\Rightarrow CD=CM\sqrt{2}=a\sqrt{2}\)
\(\Rightarrow CD^2+AC^2=AD^2\Rightarrow AC\perp CD\)
\(\Rightarrow\widehat{SCA}\) là góc giữa (SCD) và (ABCD)
\(tan\widehat{SCA}=\frac{SA}{AC}=\sqrt{2}\Rightarrow\widehat{SCA}\approx54^044'\)
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 4 2020
a. Chắc bạn ghi nhầm đề, AH và AK cắt nhau tại A trong khi BC ko đi qua A nên 3 đường này ko thể đồng quy
b. Ta có: \(CH\perp AB\) (do H là trực tâm)
\(SA\perp CH\) (do SA vuông góc mặt đáy)
\(\Rightarrow CH\perp\left(SAB\right)\Rightarrow\left(SAB\right)\perp\left(CHK\right)\)
Do \(CH\perp\left(SAB\right)\Rightarrow CH\perp SB\)
Mà \(SB\perp CK\) (K là trực tâm SBC)
\(\Rightarrow SB\perp\left(CHK\right)\Rightarrow\left(SBC\right)\perp\left(CHK\right)\)
c/ Gọi M là giao điểm AH với BC
\(\Rightarrow BC\perp\left(SAM\right)\Rightarrow\left(SBC\right)\perp\left(SAM\right)\)
Mà \(\left(SAM\right)\cap\left(CHK\right)=HK\)
\(\Rightarrow HK\perp\left(SBC\right)\)
12 tháng 8 2022
a: Xét ΔAMB và ΔAMC có
AB=AC
AM chung
MB=MC
Do đó: ΔAMB=ΔAMC
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nen AM là đường cao
=>a//BC
H
31 tháng 3 2017
(h.3.19)
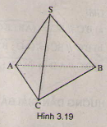
= SA.SC.cos - SA.SB.cos
= 0.
Vậy SA ⊥ BC.
\(\overrightarrow{SB}.\overrightarrow{AC}=\overrightarrow{SB}\left(\overrightarrow{SC}-\overrightarrow{SA}\right)=\overrightarrow{SB}.\overrightarrow{SC}-\overrightarrow{SB}.\overrightarrow{SA}\)
\(=SB.SC.cos\widehat{BSC}-SB.SA.cos\widehat{BSA}=0\).
Vậy \(SB\perp AC\).
\(\overrightarrow{SC}.\overrightarrow{AB}=\overrightarrow{SC}.\left(\overrightarrow{SB}-\overrightarrow{SA}\right)=\overrightarrow{SC}.\overrightarrow{SB}-\overrightarrow{SC}.\overrightarrow{SA}\)
\(=SC.SB.cos\widehat{BSC}-SC.SA.cos\widehat{CSA}=0\).
Vậy \(SC\perp AB\).
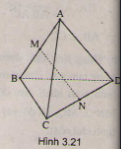
Xét \(\Delta ABD\) và \(\Delta ACD\) có:
\(AB=AC\left(gt\right)\)
\(BD=CD\left(gt\right)\)
\(AD\) là cạnh chung
\(\Rightarrow\Delta ABD=\Delta ACD\left(c.c.c\right)\)
\(\Rightarrow\widehat{BAD}=\widehat{CAD}\) (2 góc tương ứng)
Gọi giao điểm của \(AD\) và \(BC\) là \(I\)
Xét \(\Delta ABI\) và \(\Delta ACI\) có:
\(AB=AC\left(gt\right)\)
\(AI\) là cạnh chung
\(\widehat{BAI}=\widehat{CAI}\left(cmt\right)\)
\(\Rightarrow\Delta ABI=\Delta ACI\left(c.g.c\right)\)
\(\Rightarrow\widehat{AIB}=\widehat{AIC}\) (2 góc tương ứng)
Mà \(\widehat{AIB}+\widehat{AIC}=180^0\) (2 góc kề bù)
\(\Rightarrow\widehat{AIB}+\widehat{AIB}=180^0\)
\(\Rightarrow2.\widehat{AIB}=180^0\Rightarrow\widehat{AIB}=90^0\)
\(\Rightarrow AD\perp BC\left(đpcm\right)\)
camon ạ ...........!