
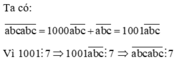
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

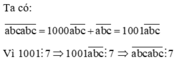

Vì 13 là lẻ \(\Rightarrow\) 13, 132, 133, 134, 135, 136 là lẻ.
Mà lẻ + lẻ + lẻ + lẻ + lẻ + lẻ = chẵn nên 13 + 132 + 133 + 134 + 135 + 136 là chẵn. \(\Rightarrow\) 13 + 132 + 133 + 134 + 135 + 136 \(⋮\) 2
\(\Rightarrow\) ĐPCM

abc = 100a + 10b + c mà x ≥1và x + y + z = 7
=> 100(a + b + c) = 100a + 100b + 100c = 700
=> abc = 100a + 10b + c = 700 - 90b - 99c = 700 - 91b - 98c + b - c = 7(100 - 13b - 14c) + (b - c) chia hết cho 7
=> b - c chia hết cho 7 nhưng b,c là 2 chữ số thỏa mãn :0
≤b + c < a + b + c = 7 => 0≤b+c≤6
=> b - c chia hết cho 7 chỉ khi b - c = 0 <=> b = c (đpcm)

abc = 100a + 10b + c mà x ≥1và x + y + z = 7
=> 100(a + b + c) = 100a + 100b + 100c = 700
=> abc = 100a + 10b + c = 700 - 90b - 99c = 700 - 91b - 98c + b - c = 7(100 - 13b - 14c) + (b - c) chia hết cho 7
=> b - c chia hết cho 7 nhưng b,c là 2 chữ số thỏa mãn :0 ≤b + c < a + b + c = 7 => 0≤b+c≤6
=> b - c chia hết cho 7 chỉ khi b - c = 0 <=> b = c (đpcm)
Ta có \(\overline{abc}=100a+10b+c⋮7\)
Do \(a+b+c⋮7\Rightarrow100a+100b+100c⋮7\)
\(\Rightarrow\left(100a+10b+c\right)+90b+99c⋮7\)
\(\Rightarrow90b+99c⋮7\Rightarrow9\left(10b+11c\right)⋮7\)
\(\Rightarrow10b+11c⋮7\Rightarrow\left(7b+14c\right)+\left(3b-3c\right)⋮7\)
\(\Rightarrow b-c⋮7\) với mọi b, c thỏa mãn điều kiện của đề bài.
Vậy thì b - c = 0 hay b = c.

abc= 100a+10b+c=(98a+7b)+2a+3b+c=7 (14a+b)+2(a+b+c) +(b-c) chia hết cho 7 khi b-c chia hết cho 7
+Nếu c =0 => b=7=> a= 7
+Nếu c=1 =>b=8 => a =5
+Nếu c=2 => b= 9 => a =3
+Hoặc b =c

A = 2+21+22+23+...+260
A = 2+2+2.2+2.2.2+........+2.2.2............2
Vì tất cả các số của tổng A là 2=> A chia hết cho 2
b) A = 2+21+22+23+...+260
A = 2. ( 1+1+22+23)+ 25 . ( 1+1+22+23)+ ..........+ 256. ( 1+1+22+23)
A = 2.14+ 25.14+..........+256.14
A= 14. ( 2+ 25+.........+256) A chia hết cho 7 vì 14 chia hêt cho 7
c) A = 2+21+22+23+...+260
A = 2. ( 1+1+22+23+ 24)+ 26 . ( 1+1+22+23+ 24)+ ..........+ 255. ( 1+1+22+23+ 24)
A = 2.30+ 26.30+..........+255.30
A= 30. ( 2+ 26+.........+255) A chia hết cho 15 vì 30 chia hết cho 15

a/
\(\overline{aba}=101.a+10b=98a+3a+7b+3b=\)
\(=\left(98a+7b\right)+3\left(a+b\right)\)
\(98a+7b⋮7;\left(a+b\right)⋮7\Rightarrow3\left(a+b\right)⋮7\)
\(\Rightarrow\overline{abc}=\left(98a+7b\right)+3\left(a+b\right)⋮7\)
b/ xem lại đề bài

a,cho abc=700
2.7+3.0+0=14
14 chia hết cho 7
b,như câu a nhưng ngược lại
cái này là mình chưa chắc đâu đấy nên đừng nói mình nha

1. \(A=2^{2016}-1\)
\(2\equiv-1\left(mod3\right)\\ \Rightarrow2^{2016}\equiv1\left(mod3\right)\\ \Rightarrow2^{2016}-1\equiv0\left(mod3\right)\\ \Rightarrow A⋮3\)
\(2^{2016}=\left(2^4\right)^{504}=16^{504}\)
16 chia 5 dư 1 nên 16^504 chia 5 dư 1
=> 16^504-1 chia hết cho 5
hay A chia hết cho 5
\(2^{2016}-1=\left(2^3\right)^{672}-1=8^{672}-1⋮7\)
lý luận TT trg hợp A chia hết cho 5
(3;5;7)=1 = > A chia hết cho 105
2;3;4 TT ạ !!