
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hướng dẫn giải:
Gọi ƯCLN của 2n + 1 và 5n + 3 là d
⇒ (2n +1)⋮ d và (5n + 3)⋮ d
⇒ [2(5n + 3) - 5(2n + 1) ] ⋮ d
⇒ 1 ⋮ d, với ∀n ∈ N
⇒ d = 1 hoặc d = -1
Vậy phân thức đã cho tối giản với ∀n ∈ N

Hướng dẫn giải:
Gọi d là ƯCLN của 7n - 5 và 3n - 2
⇒ (7n - 5)⋮ d và (3n - 2)⋮ d
⇒ [3(7n - 5) - 7(3n - 2)] = -1⋮ d
⇒ d = 1 hoặc d = -1
Vậy phân thức đã cho tối giản với ∀n ∈ N

Hướng dẫn giải:
Gọi ƯCLN của –n + 3 và n - 4 là d
⇒ (-n + 3)⋮ d và (n - 4)⋮ d
⇒ [(-n + 3) +(n - 4)] ⋮ d
⇒ -1⋮ d
⇒ d = 1 hoặc d = -1
Vậy phân thức đã cho là tối giản với ∀n ∈ N

Hướng dẫn giải:
Gọi d là ƯCLN của 3n - 2 và 4n - 3
⇒ (3n - 2)⋮ d và (4n - 3)⋮ d
⇒ [3(4n - 3) - 4(3n - 2)] = -1⋮ d
⇒ d = 1 hoặc d = -1
Vậy phân thức đã cho tối giản với ∀n ∈ N

Hướng dẫn giải:
Gọi d là ƯCLN của 3n - 2 và 4n - 3
⇒ (3n - 2)⋮ d và (4n - 3)⋮ d
⇒ [3(4n - 3) - 4(3n - 2)] = -1⋮ d
⇒ d = 1 hoặc d = -1
Vậy phân thức đã cho tối giản với ∀n ∈ N


Gọi d=ƯCLN(-n+3,n-4)
\(\Rightarrow-n+3⋮d;n-4⋮d\\ \Rightarrow-n+3+n-4⋮d\\ \Rightarrow-1⋮d\\ \Rightarrow d=1\\ \RightarrowƯCLN\left(-n+3,n-4\right)=1\)
Vậy ...

Hướng dẫn giải:
Gọi d là ƯCLN của 2n + 5 và 3n + 7
⇒ (2n + 5)⋮ d và (3n + 7)⋮ d
⇒ [3(2n + 5) - 2(3n + 7)] = 1⋮ d
⇒ d = 1 hoặc d = -1
Vậy phân thức đã cho tối giản với ∀n ∈ N

Hướng dẫn giải:
Giả sử m, n là các số nguyên và ƯCLN(m, n) = 1 (vì 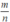 tối giản)
tối giản)
nếu d là ước chung m của m + n thì:
(m + n) d và m d
⇒ [(m + n) – m ] = n d
⇒ d ∈ ƯC (m,n) ⇒ d = 1(vì 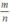 tối giản) .
tối giản) .
Vậy nếu phân thức 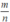 là phân thức tối giản thì phân thức
là phân thức tối giản thì phân thức 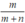 cũng là phân thức tối giản.
cũng là phân thức tối giản.
Hướng dẫn giải:
Gọi ƯCLN của 2n + 1 và 5n + 3 là d
⇒ (3n + 1) ⋮ d và (5n + 2) ⋮ d
⇒ [3(5n + 2) - 5(3n + 1)] ⋮ d
⇒ 1 ⋮ d, với ∀n ∈ N
⇒ d = 1 hoặc d = -1
Vậy phân thức đã cho tối giản với ∀n ∈ N