K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
13 tháng 1
Thay x=1 vào pt ta được pt ẩn m: 1-2(m-1).1+m=0
<=> 1 - 2m + 2 + m = 0
<=> m=3
Thay m=3 vào pt đầu và được: x2 - 4x + 3 = 0
<=> x2 - x - 3x + 3 =0
<=> x(x-1) - 3(x-1)=0
<=> (x-3) (x-1)=0
<=> x-3=0 hoặc x-1=0
<=> x=3 hoặc x=1
Vậy: Khi x=1 thì m=3, nghiệm còn lại của pt là x=3
13 tháng 5 2022
Cho phương trình \(ax^2+bx+c=0\left(a< >0\right)\)
\(\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2-4x_1x_2=\left(-\dfrac{b}{a}\right)^2-\dfrac{4c}{a}\)
\(x_1x_2=\dfrac{c}{a};x_1+x_2=-\dfrac{b}{a}\)
12 tháng 1
Bài 5:
\(x^2+2mx+2m-6=0\)
\(\text{Δ}=\left(2m\right)^2-4\left(2m-6\right)\)
\(=4m^2-8m+24\)
\(=4m^2-8m+4+20\)
\(=\left(2m-2\right)^2+20>=20>0\forall m\)
=>Phương trình luôn có hai nghiệm phân biệt
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=\dfrac{-2m}{1}=-2m\\x_1x_2=\dfrac{c}{a}=\dfrac{2m-6}{1}=2m-6\end{matrix}\right.\)
\(x_1^2+x_2^2=2x_1x_2+20\)
=>\(\left(x_1+x_2\right)^2-2x_1x_2-2x_1x_2=20\)
=>\(\left(-2m\right)^2-4\left(2m-6\right)=20\)
=>\(4m^2-8m+24-20=0\)
=>\(4m^2-8m+4=0\)
=>\(\left(2m-2\right)^2=0\)
=>2m-2=0
=>2m=2
=>m=1(nhận)
Câu 4:
a: \(2x^2-2x-m=0\)
\(\text{Δ}=\left(-2\right)^2-4\cdot2\cdot\left(-m\right)\)
\(=4+8m\)
Để phương trình có hai nghiệm phân biệt thì 8m+4>0
=>8m>-4
=>\(m>-\dfrac{1}{2}\)
b: Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-b}{a}=\dfrac{-\left(-2\right)}{2}=\dfrac{2}{2}=1\\x_1x_2=\dfrac{c}{a}=\dfrac{-m}{2}\end{matrix}\right.\)
\(\left(1-x_1x_2\right)^2+4\cdot\left(x_1^2+x_2^2\right)=16\)
=>\(\left(1+\dfrac{m}{2}\right)^2+4\cdot\left[\left(x_1+x_2\right)^2-2x_1x_2\right]=16\)
=>\(\left(\dfrac{m+2}{2}\right)^2+4\left[1^2-2\cdot\dfrac{-m}{2}\right]=16\)
=>\(\dfrac{1}{4}\left(m^2+4m+4\right)+4\left(1+m\right)=16\)
=>\(\dfrac{1}{4}m^2+m+1+4+4m-16=0\)
=>\(\dfrac{1}{4}m^2+5m-11=0\)
=>\(m^2+20m-44=0\)
=>(m+22)(m-2)=0
=>\(\left[{}\begin{matrix}m+22=0\\m-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=-22\left(loại\right)\\m=2\left(nhận\right)\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 1
5.
\(\Delta'=1+2m\)
a.
Phương trình có 2 nghiệm pb khi:
\(1+2m>0\Rightarrow m>-\dfrac{1}{2}\)
b.
Khi pt có 2 nghiệm, theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=1\\x_1x_2=-\dfrac{m}{2}\end{matrix}\right.\)
\(\left(1-x_1x_2\right)^2+4\left(x_1^2+x_2^2\right)=16\)
\(\Leftrightarrow\left(1-x_1x_2\right)^2+4\left(x_1+x_2\right)^2-8x_1x_2=16\)
\(\Leftrightarrow\left(1+\dfrac{m}{2}\right)^2+4.1^2+4m=16\)
\(\Leftrightarrow\dfrac{m^2}{4}+5m-11=0\Rightarrow\left[{}\begin{matrix}m=2\\m=-22< -\dfrac{1}{2}\left(loại\right)\end{matrix}\right.\)
5.
\(\Delta'=m^2-\left(2m-6\right)=\left(m-1\right)^2+5>0;\forall m\)
Pt luôn có 2 nghiệm pb
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-2m\\x_1x_2=2m-6\end{matrix}\right.\)
\(x_1^2+x_2^2=2x_1x_2+20\)
\(\Leftrightarrow\left(x_1+x_2\right)^2=4x_1x_2+20\)
\(\Leftrightarrow4m^2=4\left(2m-6\right)+20\)
\(\Leftrightarrow m^2-2m+1=0\Rightarrow m=1\)
C
1
AH
Akai Haruma
Giáo viên
29 tháng 10 2023
Nếu chứng minh $\sqrt{x}+\sqrt{x+1}=1$ thì không có đủ cơ sở để cm bạn nhé. Bạn viết lại đề hoặc bổ sung thêm điều kiện để mọi người trợ giúp tốt hơn.
5 tháng 6 2023
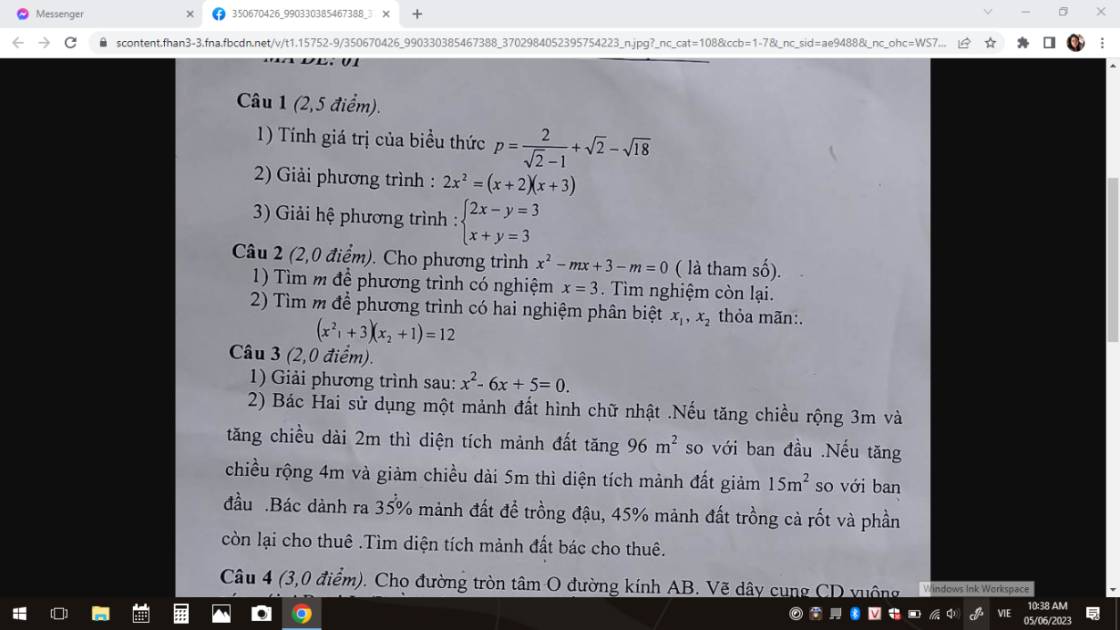
\(\Delta=b^{^2}-4ac=m^{^2}-4\left(3-m\right)=m^{^2}-12+4m=\left(m+2\right)^{^2}-16\)
Phương trình có hai nghiệm phân biệt khi và chỉ khi:
\(\Delta>0\Leftrightarrow\left(m+2\right)^2-16>0\Leftrightarrow m+2>16\Leftrightarrow m>14\\ Viete:\\ x_1+x_2=-\dfrac{b}{a}=m\\ x_1x_2=\dfrac{c}{a}=3-m\)
x1 là nghiệm phương trình nên:
\(x_1^2=mx_1+m-3=m\left(x_1+1\right)-3\\ \Rightarrow\left[m\left(x_1+1\right)-3+3\right]\left(x_2+1\right)=12\\ m\left(x_1+1\right)\left(x_2+1\right)=12\\ m\left(x_1x_2+x_1+x_2+1\right)=12\\ m\left(3-m+m+1\right)=12\\ 4m=12\\ m=3\left(KTM\right)\)
Vậy không tồn tại m thoả đề bài
PT
1
CM
15 tháng 10 2017
x2 + 7x + 12 = 0
Có a = 1; b = 7; c = 12
⇒ Δ = b2 – 4ac = 72 – 4.1.12 = 1 > 0
⇒ Phương trình có hai nghiệm phân biệt x1; x2 thỏa mãn:
Vậy dễ dàng nhận thấy phương trình có hai nghiệm là -3 và -4.
PT
1
CM
2 tháng 6 2017
x2 – 7x + 12 = 0
Có a = 1; b = -7; c = 12
⇒ Δ = b2 – 4ac = (-7)2 – 4.1.12 = 1 > 0
⇒ Phương trình có hai nghiệm phân biệt x1; x2 thỏa mãn:
Vậy dễ dàng nhận thấy phương trình có hai nghiệm là 3 và 4.
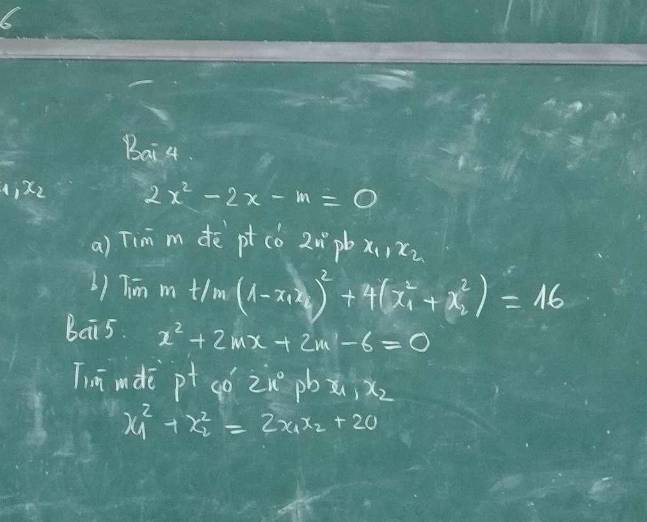
bạn có thể nói rỏ hơn không
Dễ mà bạn . Hệ thức Vi-et : cho pt bậc 2 : ax2 + bx + c = 0 (a khác 0) có 2 nghiệm x1 ; x2 thì
\(\hept{\begin{cases}x_1+x_2=-\frac{b}{a}\\x_1x_2=\frac{c}{a}\end{cases}}\)
Ta có: \(\Delta=b^2-4ac\)
Pt có 2 nghiệm \(x_1=\frac{-b-\sqrt{\Delta}}{2a}\)
\(x_2=\frac{-b+\sqrt{\Delta}}{2a}\)
Khi đó: \(x_1+x_2=\frac{-b-\sqrt{\Delta}-b+\sqrt{\Delta}}{2a}=\frac{-2b}{2a}=-\frac{b}{a}\)
\(x_1x_2=\frac{\left(-b-\sqrt{\Delta}\right)\left(-b+\sqrt{\Delta}\right)}{4a^2}=\frac{b^2-\Delta}{4a^2}\)
\(=\frac{b^2-b^2+4ac}{4a^2}=\frac{4ac}{4a^2}=\frac{c}{a}\)
Vậy.............